如图,在菱形 中, , 交 的延长线于点 .连结 交 于点 ,交 于点 . 于点 ,连结 .有下列结论:① ;② ;③ ;④ .其中所有正确结论的序号为 .

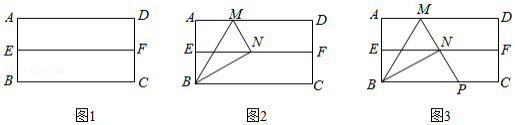
如图,在矩形 中, ,对角线相交于点 ,动点 从点 向点 运动(到点 即停止),点 是 上一动点,且满足 ,连结 .在点 、 运动过程中,则以下结论正确的是 .(写出所有正确结论的序号)
①点 、 的运动速度不相等;
②存在某一时刻使 ;
③ 逐渐减小;
④ .
如图, 是 的直径, , 是 的弦, 为 的中点, 与 交于点 ,过点 作 ,交 的延长线于点 ,且 平分 .
(1)求证: 是 的切线;
(2)求证: ;
(3)若 , ,求 的长.

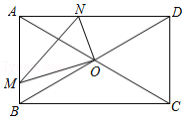
已知,在 中, , .

(1)如图1,已知点 在 边上, , ,连结 .试探究 与 的关系;
(2)如图2,已知点 在 下方, , ,连结 .若 , , , 交 于点 ,求 的长;
(3)如图3,已知点 在 下方,连结 、 、 .若 , , , ,求 的值.
在 中, ,有一个锐角为 , .若点 在直线 上(不与点 , 重合),且 ,则 的长为 .
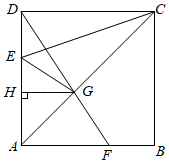
由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中 的长应是 .

如图1, 为 上一点,点 在直径 的延长线上,且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求 的半径;
(3)如图2,在(2)的条件下, 的平分线 交 于点 ,交 于点 ,连结 .求 的值.

如图,在 中, , , ,点 从点 出发沿 方向运动,到达点 时停止运动,连结 ,点 关于直线 的对称点为 ,连结 , .在运动过程中,点 到直线 距离的最大值是 ;点 到达点 时,线段 扫过的面积为 .

如图,点 在正方形 边 上,点 是线段 上的动点(不与点 重合), 交 于点 , 于点 , , .
(1)求 ;
(2)设 , ,试探究 与 的函数关系式(写出 的取值范围);
(3)当 时,判断 与 的位置关系并说明理由.
如图,已知正方形 边长为1, 为 边上一点,以点 为中心,将 按逆时针方向旋转得 ,连接 ,分别交 , 于点 , .若 ,则 .

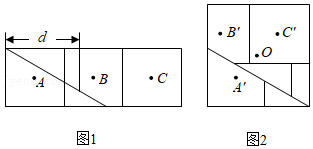
图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图 ,则图1中所标注的 的值为 ;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为 .
如图,先将矩形纸片 沿 折叠 边与 在 的异侧), 交 于点 ;再将纸片折叠,使 与 在同一条直线上,折痕为 .若 ,纸片宽 ,则 .

已知在 中, 是 的中点, 是 延长线上的一点,连结 , .

(1)如图1,若 , , , ,求 的长.
(2)过点 作 ,交 延长线于点 ,如图2所示,若 , ,求证: .
(3)如图3,若 ,是否存在实数 ,当 时, ?若存在,请写出 的值;若不存在,请说明理由.
如图,点 在以 为直径的 上,过 作 的切线交 延长线于点 , 于点 ,交 于点 ,连接 , .
(1)求证: ;
(2)求证: ;
(3)若 , ,求 的长.

在我们学习过的数学教科书中,有一个数学活动,若身旁没有量角器或三角尺,又需要作 , , 等大小的角,可以采用如下方法:
操作感知:
第一步:对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开(如图1 .
第二步:再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 (如图 .
猜想论证:
(1)若延长 交 于点 ,如图3所示,试判定 的形状,并证明你的结论.
拓展探究:
(2)在图3中,若 , ,当 , 满足什么关系时,才能在矩形纸片 中剪出符合(1)中结论的三角形纸片 ?