如图,在 中,直径 经过弦 的中点 ,点 在 上, 的延长线交 于点 ,交过 的直线于 , ,连接 与 交于点 .
(1)求证: 是 的切线;
(2)若点 是 的中点, 的半径为3, ,求 的长.

在矩形ABCD中,E为CD的中点,H为BE上的一点, ,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: ;
(2)若∠CGF=90°,求 的值.

如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.

如图,在 中, , 是 上一点,过 , , 三点的 交 于点 ,连接 , ,点 是线段 上的一点,连接 ,其中 .
(1)求证: 是 的切线.
(2)若 是 的中点, , ,求 的长.

如图, 和 是有公共顶点的等腰直角三角形, ,点 为射线 , 的交点.
(1)求证: ;
(2)若 , ,把 绕点 旋转,当 时,求 的长;
如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PA•PC,连接CE,AE,OE,OE交CA于点D.
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°, ,求证:DO=DP.

如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若 ,AE=4,求CD.

如图,四边形 是菱形,点 为对角线 的中点,点 在 的延长线上, ,垂足为 ,点 在 的延长线上, ,垂足为 ,
(1)若 ,求证:四边形 是菱形;
(2)若 , 的面积为16,求菱形 的面积.
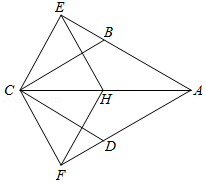
如图,已知 、 为 的两条直径, 为切线,过 上一点 作 于 ,连接 并延长交 于点 ,连接 .
(1)求证: .
(2)设 为点 关于 对称点,连接 、 ,如果 , 的半径为3,求 的值.

如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.

如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D,E为 的中点,连接CE,BE,BE交AC于F.
(1)求证:AB=AF;
(2)若AB=3,BC=4,求CE的长.

如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.

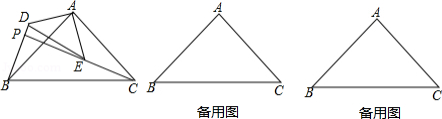
教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
例2 如图,在中,
,
分别是边
,
的中点,
,
相交于点
,求证:
证明:连结.
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:在中,对角线
、
交于点
,
为边
的中点,
、
交于点
.
(1)如图②,若为正方形,且
,则
的长为 .
(2)如图③,连结交
于点
,若四边形
的面积为
,则
的面积为 .
如图,小明在笔直的河岸上的点
处,以正对岸明显的标志点
为参照点,设计出两种测量河宽
的方案,绘制了相应的示意图,并用测角仪、卷尺及标杆测得一些数据如下:

(1)请你选择一种方案,结合示意图,简述测量过程;
(2)按照你选定的方案,求河宽.(参考数据:
,