初中数学中心对称图形解答题

在四张背面完全相同的纸牌A、B、C、D，其中正面分别画有四个不同的几何图形（如图），小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸一张．

（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌可用A、B、C、D表示）；

（2）求摸出两张纸牌牌面上所画几何图形，既是轴对称图形又是中心对称图形的概率．

如图10所示，Rt△ABC是一张放在平面直角坐标系中的纸片，点C与原点O重合，点A在x轴的正半轴上，点B在y轴的正半轴上，已知OA=3，OB＝4。将纸片的直角部分翻折，使点C落在AB边上，记为D点，AE为折痕，E在y轴上。
（1）在图10所示的直角坐标系中，求E点的坐标及AE的长。
（2）线段AD上有一动点P（不与A、D重合）自A点沿AD方向以每秒1个单位长度向D点作匀速运动，设运动时间为t秒（0<t<3），过P点作PM∥DE交AE于M点，过点M作MN∥AD交DE于N点，求四边形PMND的面积S与时间t之间的函数关系式，当t取何值时，S有最大值？最大值是多少？
（3）当t（0<t<3）为何值时，A、D、M三点构成等腰三角形？并求出点M的坐标。

（本题10分）如图，在直角梯形ABCD中，AB∥DC，∠D=90^o，AC⊥BC，AB=10cm,BC=6cm，F点以2cm／秒的速度在线段AB上由A向B匀速运动，E点同时以1cm／秒的速度在线段BC上由B向C匀速运动，设运动时间为t秒(0<t<5)．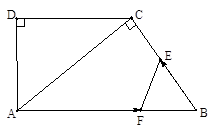

（1）求证：△ACD∽△BAC；
（2）求DC的长；
（3）设四边形AFEC的面积为y，求y 关于t的函数关系式，并求出y的最小值．

在Rt△ACB中，∠C=90°，AC=3cm，BC=4cm，以BC为直径作⊙O交AB于点D.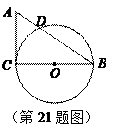

（1）求线段AD的长度；
（2）点E是线段AC上的一点，试问当点E在什么位置时，直线ED与⊙O相切？请说明理由.

如图，一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合，过E点作EF⊥AE交∠DCE的角平分线于F点，试探究线段AE与EF的数量关系，并说明理由。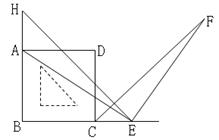

第18题图

如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.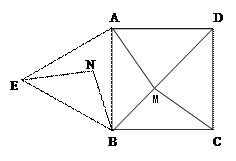

⑴ 求证：△AMB≌△ENB；
⑵ ①当M点在何处时，AM＋CM的值最小；
②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；
⑶ 当AM＋BM＋CM的最小值为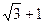时，求正方形的边长.

图3.1、图3.2、图3.3均是单位为1的方格图.
（1）请把方格图3.1中的带阴影的图形适当剪开，重新拼成正方形；（画出分割线，在图3.2中画出拼成正方形的草图）
（2）所拼成正方形的边长为多少？周长为多少?
（3）利用这个事实，在图3.3的数轴上画出表示的点A.（要求保留画图痕迹）
（4）在图3.3的数轴上画出表示的点B.（要求保留画图痕迹）

(7分)如图，D是△ABC的边AB上一点，DF交AC于点E，DE=FE，FC∥AB，
求证：AD=CF．

如图，在直角坐标系中， $\text{Rt}\Delta \text{ABC}$的直角边 $\mathit{AC}$在 $x$轴上， $\angle \mathit{ACB}=90°$， $\mathit{AC}=1$，反比例函数 $y=\frac{k}{x}(k>0)$的图象经过 $\mathit{BC}$边的中点 $D(3,1)$．

（1）求这个反比例函数的表达式；

（2）若 $\mathit{\Delta ABC}$与 $\mathit{\Delta EFG}$成中心对称，且 $\mathit{\Delta EFG}$的边 $\mathit{FG}$在 $y$轴的正半轴上，点 $E$在这个函数的图象上．

①求 $\mathit{OF}$的长；

②连接 $\mathit{AF}$， $\mathit{BE}$，证明四边形 $\mathit{ABEF}$是正方形．

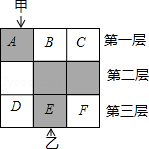
如图， $3\times 3$的方格分为上中下三层，第一层有一枚黑色方块甲，可在方格 $A$、 $B$、 $C$中移动，第二层有两枚固定不动的黑色方块，第三层有一枚黑色方块乙，可在方格 $D$、 $E$、 $F$中移动，甲、乙移入方格后，四枚黑色方块构成各种拼图．

（1）若乙固定在 $E$处，移动甲后黑色方块构成的拼图是轴对称图形的概率是　　．

（2）若甲、乙均可在本层移动．

①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率．

②黑色方块所构拼图是中心对称图形的概率是　　．

（本小题满分5分）
如图，梯形ABCD中，AB∥CD，F是DC的中点，BF的延长线交射线AD于点G,， BG 交AC于点E．求证：=．

（本小题满分5分）
如图，在梯形中，，，，，  
，求的长．

（1）请画出关于轴对称的
（其中分别是的对应点，不写画法）；

（2）直接写出三点的坐标：
．
（3）计算△ABC的面积．

如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，
（1）写出图中一对全等的三角形，并写出它们的所有对应角；
（2）设的度数为x，∠的度数为，那么∠1，∠2的度数分别是多少？（用含有x或y的代数式表示）
（3）∠A与∠1+∠2之间有一种数量关系始终保持不变，请找出这个规律．

(9分) 如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，
BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M。
（1）求证：MB=MD，ME=MF
（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由。