如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥OC,
OC与BD交于E,若AO=2,BC=2 ,求:
,求:
(1)求∠A的度数;(2)求DE的长
规定:在平面内,如果一个图形绕一个定点旋转一定的角度 后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度 称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点 旋转 或 后,能与自身重合(如图 ,所以正方形是旋转对称图形,且有两个旋转角.
根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是 ;
.矩形
.正五边形
.菱形
.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有: (填序号);
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形.
其中真命题的个数有 个;
.0
.1
.2
.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有 , , , ,将图形补充完整.

(本题10分)如图,在直角梯形ABCD中,AB∥DC,∠D=90o,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).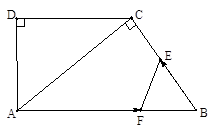
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y 关于t的函数关系式,并求出y的最小值.
如图10所示,Rt△ABC是一张放在平面 直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
(1)在图10所示的直角坐标系中,求E点的坐标及AE的长。
(2)线段AD上有一动点P(不与A、D重合)自A点沿AD方向以每秒1个单位长度向D点作匀速运动,设运动时间为t秒(0<t<3),过P点作PM∥DE交AE于M点,过点M作MN∥AD交DE于N点,求四边形PMND的面积S与时间t之间的函数关系式,当t取何值时,S有最大值?最大值是多少?
(3)当t(0<t<3)为何值 时,A、D、M三点构成等腰三角形?并求出点M的坐标。
时,A、D、M三点构成等腰三角形?并求出点M的坐标。
在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.

如图,在△ABC中,BC>AC,点D在BC上,且DC=AC.
(1)利用直尺与圆规先作∠ACB的平分线,交AD于F点,再作线段AB的垂直
平分线,交AB于点E,最后连结EF(保留作图痕迹,不要求写作法、证明).
(2)若线段AC= 8,BC= 12,求线段EF的长.
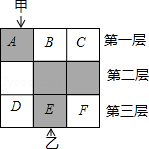
如图, 的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格 、 、 中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格 、 、 中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
(1)若乙固定在 处,移动甲后黑色方块构成的拼图是轴对称图形的概率是 .
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率.
②黑色方块所构拼图是中心对称图形的概率是 .

(本小题满分10分)
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad  的值为()
的值为()
A. |
B.1 | C. |
D.2 |
(2)对于 ,∠A的正对值sad A的取值范围是.
,∠A的正对值sad A的取值范围是.
(3)已知 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值.
如图,在直角坐标系中, 的直角边 在 轴上, , ,反比例函数 的图象经过 边的中点 .
(1)求这个反比例函数的表达式;
(2)若 与 成中心对称,且 的边 在 轴的正半轴上,点 在这个函数的图象上.
①求 的长;
②连接 , ,证明四边形 是正方形.

如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图 放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
试猜想线段BE和EC的数量及位置关系,并 证明你的猜想.
证明你的猜想.
如图, 的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格 、 、 中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格 、 、 中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
(1)若乙固定在 处,移动甲后黑色方块构成的拼图是轴对称图形的概率是 .
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率.
②黑色方块所构拼图是中心对称图形的概率是 .