2011年初中毕业升学考试(贵州六盘水卷)数学
下列运算正确的是()
| A.a2+a3=a5 | B. =±2 =±2 |
C.(2a)3=6a3 | D.(-3x-2)(3x-2)=4-9x2 |
下列说法正确的是( )
| A.要调查人们对“低碳生活”的了解程度,宜采用普查方式 |
| B.一组数据:3,4,4,6,8,5的众数和中位数都是3 |
| C.必然事件的概率是100%,随机事件的概率是50% |
| D.若甲组数据的方差S甲2=0.128,乙组数据的方差是S乙2=0.036,则乙组数据比甲组数据稳定 |
找出下列四句话中不相同的一句( )
| A.上海自来水来自海上 | B.有志者事竟成 |
| C.清水池里池水清 | D.蜜蜂酿蜂蜜 |
如图,把一张矩形纸片ABCD沿对角线BD折叠,使点C落
在E处,BE与AD相交于F,下列结论:①BD2=AD2+AB2 ②△ABF≌△EDF ③
②△ABF≌△EDF ③ ④AD=BD·cos45°正确的是( )
④AD=BD·cos45°正确的是( )
| A.①② | B.②③ | C.①④ | D.③④ |
如图,边长都为1的正方形和正三角形,其一边在同一水平线上,三角形沿该水平线自左向右匀速穿过正方形。设穿过的时间为
,正方形与三角形重合部分的面积为
,那么
关于
的函数大致图象应为( )
 |
如图,AD∥BC,BP平分∠ABC,AP平分∠BAD,PE⊥AB,PE=2,则两平行线AD、BC之间的距离为 
将边长分别为 ,2
,2 ,3
,3 ,
,
4 …的正方形的面积记作S1,S2,S3,
…的正方形的面积记作S1,S2,S3,
S4…,计算S2- S1,S3-S2,S4-S3…,若
边长为n (n为正整数)的正方形面积
(n为正整数)的正方形面积
记作Sn,根据你计算的规律,猜想:
Sn+1-Sn=
如图,在顶角为30°的等腰三角形ABC中,AB=AC,
若过点C作CD⊥AB于D,则∠BCD=15°,根据图形计算 tan15°=
tan15°=
如图,一次函数图象与x轴交于点B,与反比例函数图象
交于点A(1,-6),△AOB的面积为6,求一次函数和反比例函
数的解析式
为了建设社会主义新农村,华新村修筑了一条长3000m的公路,实际工作效率比原计划提高了20%,结果提前5天完成任务。问原计划每天修路多长?
根据国务院新闻办公室2011年4月28日发布的《2011年全国第六次人口普查主要数据公报(第1号)》,就全国人口受教育情况的数据绘制了条形统计图和扇形统计图如下:
根据统计图提供的信息,解答下列问题:
(1)这次人口普查统计的全国人口总数约为 亿人(精确到0.1)
(2)补全条条形统计图和扇形统计图
(3)求扇形统计图中表示“高中文化”的圆心角的度数
已知⊙O的直径AB的长为4㎝,C是⊙O上一点, ∠BAC=30°,过点C作⊙O的切线交AB的延长线于点
∠BAC=30°,过点C作⊙O的切线交AB的延长线于点
P,求BP的长
某工厂有一种材料,可加工甲、乙、丙三种型号机械配件共240件,厂方计划由20个工人一天内加工完成,并要求每人只加工一种配件,根据下表提供的信息,解答下列问题:
| 配件种类 |
甲 |
乙 |
丙 |
| 每人可加工配件的数量(个) |
16 |
12 |
10 |
| 每个配件获利(元) |
6 |
8 |
5 |
(1)设加工甲种配件的人数为x,加工乙种配件的人数为y,求y与x之间的函数关系式
(2)如果加工每种配件的人数均不少于3人,那么加工配件的人数安排方案有几种?并写出每种安排方案
(3)要使此次加工配件的利润最大,应采用哪种方案?最大利润是多少?
 |
如图①,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起
(1)操作:如图②,将△ECF的顶点F固定在△ABD的BD边上的中点处,将△ECF绕点F在BD的上方左右旋转,设旋转时FC交BA于H(不与点B重合),EF交DA于G(不与点D重合),求证:BH·GD=BF2
(2)操作:如图③,△ECF的顶点F在△ABD的BD边上滑动(不与点B、D重合),且CF如终过点A,过点A作AG∥CE,交EF于G,连接DG 探究:FD+DG= ,并请证明你的结论
探究:FD+DG= ,并请证明你的结论
 |
|||
 |
九(1)班数学课题学习小组,为了研究学习二次函数问题,他们经历了实践——应用——探究的过程
(1)实践:他们对一条公路上横截面为抛物线的单向双车道的隧道进行测量,测得隧道的路面宽为10米,隧道顶部最高处距地面6.25米,并画出了隧道截面图,建立了如图所示的直角坐标系,请你求出抛物线的解析式
(2)应用:按规定机动车辆通过隧道时,车顶部与隧道顶部在竖起方向上的高度差至少为0.5米,为了确保安全,问该隧道能否让最宽3米,最高3.5米的两辆车居中并列行驶(不考虑两车之间的空隙)?
(3)探究:该课题学习小组为进一步探究抛物线的有关知识,他们借助上述抛物线模型,提出了以下两个问题,请予解答:
①如图,在抛物线内作矩形ABCD,使顶点C、D落在抛物线上,顶点A、B落在x轴上,设矩形ABCD的周长为为l,求l的最大值
②如图,过原点作一条直线y=x,交抛物线于M,交抛物线的对称轴于N,P为直线OM上一动点,过点P作x轴的垂线交抛物线于点Q,问在直线OM上是否存在点P,使以点P、N、Q为顶点的三角形为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由
 |
图1是正方体的一个平面展开图,如果叠成原来的正方体,与“创”字相对的字是( )
| A.都 | B.美 | C.好 | D.凉 |
已知两圆的半径分别为1和2,圆心距为5,那么这两个圆的位置关系是( )
| A.内切 | B.相交 | C.外离 | D.外切 |
下列事件是必然事件的是( )
| A.若a>b,则ac>bc |
| B.在正常情况下,将水加热到1000C时水会沸腾 |
| C.投掷一枚硬币,落地后正面朝上 |
| D.长为3cm、3cm、7cm的三条线段能围成一个三角形 |
如图2,火车匀速通过隧道(隧道长等于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图像描述大致是( )
若点(-3,y1)、(-2,y2)、(1,y3)在反比例函数 的图像上,则下列结论正确的是( )
的图像上,则下列结论正确的是( )
| A.y1> y2> y3 | B.y2> y1> y3 | C.y3> y1> y2 | D.y3> y2> y1 |
“标准对数视力表”对我们来说并不陌生,图3是视力表的一部分,其中最上面较大的“E”与下面四个较小“E”中的哪一个是位似图形( )
| A.左上 | B.左下 | C.右上 | D.右下 |
如图4,在菱形ABCD中,对角线AC=6,BD=8,点E、F分别是边AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )
A.3 B.4 C.5 D.6
通过第六次全国人口普查得知,六盘水市人口总数约为2851180人,这个数用科学记数法表示是_____________人(保留两个有效数字).
在平面直角坐标系中,点P(2,3)与点 (2a+b,a+2b)关于原点对称,则a-b的值为_________
(2a+b,a+2b)关于原点对称,则a-b的值为_________
小明将两把直尺按图5所示叠放,使其中一把直尺的一个顶点恰好落在另一把直尺的边上,则∠1+∠2=_______度。
从美学角度来说,人的上身长与下身长之比为黄金比时,可以给人一种协调的美感。某女老师上身长约61.80cm,下身长约93.0 0cm,她要穿约________cm的高跟鞋才能达到黄金比的美感效果(精确到0.01cm)
0cm,她要穿约________cm的高跟鞋才能达到黄金比的美感效果(精确到0.01cm)
在我市举行的“祖国好,家乡美”唱红歌比赛活动中,共有40支参赛队。市教育局对本次活动的获奖情况进行了统计,并根据收集的数据绘制了图6、图7两幅不完整的统计图,请你根据图中提供的信息解答下面的问题:
1、获一、二、三等奖各有多少参赛队?
2、在答题卷上将统计图图6补充完整。
3、计算统计图图7中“没获将”部分所对应的圆心角的度数
4、求本次活动的获奖概率。
小明家有一块长8m、宽6m的矩形空地,妈妈准备在该空地上建造一个花园,并使花园面积为空地面积的一半,小明设计了如下的四种方案供妈妈挑选,请你选择其中的一种方案帮小明求出图中的x值。



如图8,已知:△ABC是⊙O的内接三角形,D是OA延 长线上的一点,连接DC,且∠B=∠D=300。
长线上的一点,连接DC,且∠B=∠D=300。
(1)判断直线CD与⊙O的位置关系,并说明理由。
(2)若AC=6,求图中弓形(即阴影部分)的面积。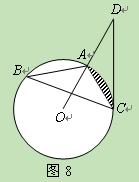
某一特殊路段规定:汽车行驶速度不超过36千米/时。一辆汽车在该路段上由东向西行驶,如图所示,在距离路边10米O处有一“车速检测仪”,测得该车从北偏东600的A点行驶到北偏东300的B点,所用时间为1秒。
(1)试求该车从A点到B点的平均速度。
(2)试说明该车是否超速。( 、
、 )
)
如图10所示,Rt△ABC是一张放在平面 直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
(1)在图10所示的直角坐标系中,求E点的坐标及AE的长。
(2)线段AD上有一动点P(不与A、D重合)自A点沿AD方向以每秒1个单位长度向D点作匀速运动,设运动时间为t秒(0<t<3),过P点作PM∥DE交AE于M点,过点M作MN∥AD交DE于N点,求四边形PMND的面积S与时间t之间的函数关系式,当t取何值时,S有最大值?最大值是多少?
(3)当t(0<t<3)为何值 时,A、D、M三点构成等腰三角形?并求出点M的坐标。
时,A、D、M三点构成等腰三角形?并求出点M的坐标。

 中自变量x的取值范围是
中自变量x的取值范围是 

 -2│-(π-3.14)0+(
-2│-(π-3.14)0+( )-1-2sin60°
)-1-2sin60°



 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( ) B
B 
 D
D 




 ,
, ,
, ,
, ……,则它的第7个数是________;第n个数是_______。
……,则它的第7个数是________;第n个数是_______。
 ,再从你
,再从你 粤公网安备 44130202000953号
粤公网安备 44130202000953号