2011年浙江省金衢十一校初三数学联考试卷
(本小题满分8分。其中(1)小题4分,(2)小题4分)
如图3:在正方形网格上有一个△ABC.
(1)作出△ABC关于直线MN的对称图形;
(2)若网格上最小正方形的边长为1,求△ABC的面积.
(本小题满分8分)列方程解应用题:
现加工一批机器零件,甲单独完成需4天,乙单独完成需6天。现由乙先做1天,然后两人合做,完成后共得报酬600元。若按个人完成的工作量给付报酬,你应如何分配呢?
(本小题满分9分,其中(1)小题5分,(2)小题4分)
如图4:在△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,点E是BC上一个动点(点E与B、C不重合),连接A、E.若a、b满足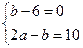 ,且c是不等式组
,且c是不等式组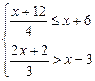 的最大整数解.
的最大整数解.
(1)求a、b、c的长.
(2)若AE平分△ABC的周长,求∠BEA的大小.
(本小题满分9分,其中(1)小题4分,(2)小题5分)
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)
| |
甲 |
乙 |
| 进价(元/件) |
15 |
35 |
| 售价(元/件) |
20 |
45 |
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?
己知1纳米=0.000000001米,则27纳米用科学记数法表示为( ).
| A.27×10-9 | B.2.7×10-8 | C.2.7×10-9 | D.-2.7×108 |
期中考试后,小明的讲义夹里放了8K大小的试卷纸共12页,其中语文4页、数学2页、英语6页,他随机从讲义夹中抽出1页,是数学卷的概率是( ).
A. |
B. |
C. |
D. |
下列命题中的真命题是( ).
| A.对角线互相垂直的四边形是菱形 | B.中心对称图形都是轴对称图形 |
| C.两条对角线相等的梯形是等腰梯形 | D.等腰梯形是中心对称图形 |
下列命题:
①若b=2a+ c,则一元二次方程a
c,则一元二次方程a +bx+c=O必有一根为-2;
+bx+c=O必有一根为-2;
②若ac<0, 则方程 c +bx+a=O有两个不等实数根;
+bx+a=O有两个不等实数根;
③若 -4ac="0," 则方程 c
-4ac="0," 则方程 c +bx+a=O有两个相等实数根;
+bx+a=O有两个相等实数根;
其中正确的个数是( )
A O个 B.l个 C.2个 D。3 个
如图,△ABC内接于⊙O,其外角平分线AD交⊙O于DM⊥AC于M,下列结论:
①DB=DC;②AC-AB=2AM;③AC+AB=2CM;④ =2
=2 其中正确的有( )
其中正确的有( )
| A.只有④② | B.只有①②③ | C.只有③④ | D.①②③④ |

如图,四个电子宠物排座位:一开始,小鼠、小猴、小兔、小猫分别坐在1、2、3、4号的座位上,以后它们不停地交换位置,第一次上下两排交换位置,第二次是在第一次交换位置后,再左右两列交换位置,第三次是在第二次交换位置后,再上下两排交换位置,第四次是在第三次交换位置后,再左右两列交换位置,…,这样一直继续交换位置,第2008次交换位置后,小鼠所在的座号是( ).
| A.1 | B.2 | C.3 | D.4 |
老师给出一个y关于x的函数,甲、乙、丙、丁四位同学各指出这个函数的一个性质:甲:函数图象不经过第三象限;乙:函数图象经过第一象限;丙:当x<2时,y随x的增大而减小;丁:当x<2时y>0.已知这四位同学叙述都正确。请写出满足上述所有性质的一个函数______________.
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的.当同时转动两个转盘,停止后指针所指的两个数字表示两条线段的长,如果第三条线段的长为5,那么这三条线段能构成三角形的概率为_____________.
如图,⊙O1和⊙O2的半径为2和3,连接O1O2,交⊙O2于点P,O1O2=7,若将⊙O1绕点 按顺时针方向以30°/秒的速度旋转一周,请写出⊙O1与⊙O2相切时的旋转时间为_______秒.
按顺时针方向以30°/秒的速度旋转一周,请写出⊙O1与⊙O2相切时的旋转时间为_______秒.
(本小题满分6分)
在如图所示的直角坐标系中,O为原点,直线 与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且
与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且 ,试求点P的坐标.
,试求点P的坐标.
.(本小题满分6分)
数学来源于生活又服务于生活,利用数学中的几何知识可以帮助我们解决许多实际问题.李明准备与朋友合伙经营一个超市,经调查发现他家附近有两个大的居民区A、B,同时又有相交的两条公路,李明想把超市建在到两居民区的距离、到两公路距离分别相等的位置上,绘制了如下的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助李明在图上确定超市的位置!请用尺规作图确定超市P的位置.(作图不写作法,但要求保留作图痕迹.)
(本小题满分8分)
为减少环境污染,自2008年6月1日起,全国的商品零售场 所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:
所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分: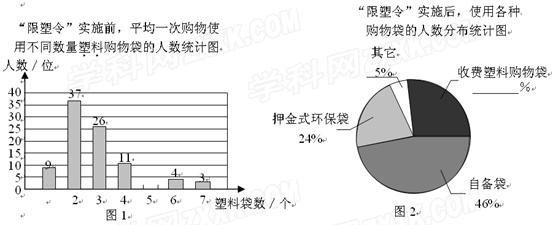
“限塑令”实施后,塑料购物袋使用后的处理方式统计表
| 处理方式 |
直接丢弃 |
直接做垃圾袋 |
再次购物使用 |
其它 |
| 选该项的人数占 总人数的百分比 |
5% |
35% |
49% |
11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料 购物袋使用后怎样处理,能对环境保护带来积极的影响.
购物袋使用后怎样处理,能对环境保护带来积极的影响.
已知Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,且AB=2A′B′,则sinA
与sinA′的关系为 ( )
| A.sinA=2sinA′ | B.sinA=sinA′ | C.2sinA=sinA′ | D.不确定 |
为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的
体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一
周参加体育锻炼时间的众数与中位数分别是 ( ) 
| A.8, 9 | B.8,8 |
| C.16,13 | D.10,9 |
如图①,有6张写有实数的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开两张都是无理数的概率是 ( )
A. |
B. |
C. |
D. |
如图,若用半径为9,圆心角为 的扇形围成一个圆锥的侧面(接缝忽略不计),
的扇形围成一个圆锥的侧面(接缝忽略不计),
则这个圆锥的底面半径是 ( )
| A.1.5 | B.2 | C.3 | D.6 |

据媒体报道,中俄原油管道于2011年1月1日正式启用,首日输送4.2万吨,
年输送1500万吨。年输油量1500万吨用科学记数法表示为 ▲ 万吨.
图中刀柄外形是一个直角梯形(下底挖去一小半圆),刀片上、下是平行的,转动刀片(如图)时形成∠1、∠2,则∠1+∠2= ▲ 度.
如图,直线 (
( >0)与双曲线
>0)与双曲线 在第一象限内的交点为R,与
在第一象限内的交点为R,与 轴
轴
的交点为P,与 轴的交点为Q;作RM⊥
轴的交点为Q;作RM⊥ 轴于点M,若△OPQ与△PRM的面积是9∶1,则
轴于点M,若△OPQ与△PRM的面积是9∶1,则 ▲ .
▲ .
如图正方形ABCD,其边长为4.P是射线AB上的点,且AP=x.将△APD沿过点D的折痕PD折叠,点A的落点记为A/,若△A/DP与正方形ABCD的重叠面积记为S,
(1)若x="6," 则S= ▲
(2) ≤S≤1时,则x的取值范围为(用含x的不等式表示)____▲ ______.
≤S≤1时,则x的取值范围为(用含x的不等式表示)____▲ ______.
如图,已知:梯形ABCD中,AD∥BC,E为对角线AC的中点,连结
DE并延长交BC于点F,连结AF.
(1)求证:AD=CF;
(2)在原有条件不变的情况下,当AC满足条件 ▲ 时(不再增添辅助线),四边形AFCD成为菱形,
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,
的三个顶点 都在格点上(每个小方格的顶点叫格点).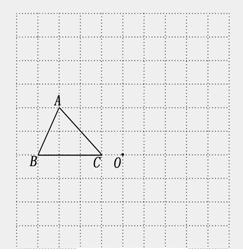
(1)画出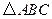 关于点
关于点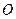 的中心对称的
的中心对称的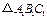 ;如果建立直角坐标系,使点B的坐标为
;如果建立直角坐标系,使点B的坐标为
(-5,2),点C的坐标为(-2,2),则点A1的坐标为 ▲ ;
(2) 画出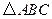 绕点
绕点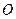 顺时针旋转
顺时针旋转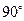 后的
后的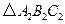 ,并求线段BC扫过的面积.
,并求线段BC扫过的面积.
如图,一部起重机的机身AD高22m,吊杆AB长40m,吊杆与水平线的夹角∠BAC可从30°升到80°.分别求起重机起吊过程中的最大水平距离和起重机起吊的离地面最大高度(吊钩本身的长度和所挂重物的高度忽略不计)。
(结果精确到0.1米,sin80°=0.9848,cos80°=0.1736, 

如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥OC,
OC与BD交于E,若AO=2,BC=2 ,求:
,求:
(1)求∠A的度数; (2)求DE的长
某年级组织学生参加数理化奥林匹克竞赛的培训,下面两幅统计图反
映了学生自愿报名(每人限报一科)的情况,请你根据图中信息回答下列问题:
(1)该年级报名参加数学培训的人数有 ▲ .
(2)该年级报名参加这三科奥训的总人数是 ▲ .请补全条形统计图.
(3)根据实际情况,需从数学组抽调部分同学到化学组,使化学组人数是数学组人数的3倍,则应从数学组抽调多少名学生?
 如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与
如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与 轴交于点A,
轴交于点A,
过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得 到抛物线F ′:
到抛物线F ′:
y=a′x2+b′x+c′,抛物线F ′与x轴的另一个交点为C.
(1)当a=1,b=-2,c=3时,
①写出点D的坐标 ▲ ;②求b:  的值;
的值;
(2)若a、b、c满足b2=ac,探究b:  的值是否为定值?若是定值请求出这个定值;若不是请说明理由.
的值是否为定值?若是定值请求出这个定值;若不是请说明理由.
已知,边长为5的正方形ABCO在如图所示的直角坐标系中,点
M(t,0)为x轴上一动点,过A作直线MC的垂线交y轴于点N.
(1)当t=2时,求直线MC的解析式;
(2)设△AMN的面积为S,当S=3时,求t的值;
(3)取点P(1,y),如果存在以M、N、C、P为顶点的四边形是等腰梯形,当t<0时,甲同学说:y与t应同时满足方程t2-yt-5=0和y2-2t2-10y+26=0;乙同学说:y与t应同时满足方程t2-yt-5=0和y2+8t-24=0,你认为谁的说法 正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.

 , ∠B=30°, 则DE的长是( ).
, ∠B=30°, 则DE的长是( ).







 B.
B.  C.
C.  D. 8
D. 8  ,且
,且 ,则b= .
,则b= . ,则其侧面积为
,则其侧面积为

 ,其中
,其中




 的图象如图所示
的图象如图所示 ,则一次函数
,则一次函数 与反比例函数
与反比例函数 在同一坐标系内的图象大致为 ( )
在同一坐标系内的图象大致为 ( )
 = ▲ .
= ▲ . 中自变量
中自变量 的取值范围是 ▲ .
的取值范围是 ▲ . .
. =0
=0  粤公网安备 44130202000953号
粤公网安备 44130202000953号