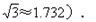如图，一部起重机的机身ＡＤ高22m，吊杆AB长40m，吊杆与水平线的夹角∠BAC可从30°升到80°．分别求起重机起吊过程中的最大水平距离和起重机起吊的离地面最大高度（吊钩本身的长度和所挂重物的高度忽略不计）。
（结果精确到0.1米，sin80°=0.9848，cos80°=0.1736，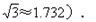 
；
．
+
）0+
+（-1）2015-
tan60°．相关知识点
推荐套卷
如图，一部起重机的机身ＡＤ高22m，吊杆AB长40m，吊杆与水平线的夹角∠BAC可从30°升到80°．分别求起重机起吊过程中的最大水平距离和起重机起吊的离地面最大高度（吊钩本身的长度和所挂重物的高度忽略不计）。
（结果精确到0.1米，sin80°=0.9848，cos80°=0.1736，
粤公网安备 44130202000953号