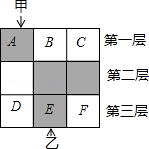
如图， 的方格分为上中下三层，第一层有一枚黑色方块甲，可在方格 、 、 中移动，第二层有两枚固定不动的黑色方块，第三层有一枚黑色方块乙，可在方格 、 、 中移动，甲、乙移入方格后，四枚黑色方块构成各种拼图．
（1）若乙固定在 处，移动甲后黑色方块构成的拼图是轴对称图形的概率是 ．
（2）若甲、乙均可在本层移动．
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率．
②黑色方块所构拼图是中心对称图形的概率是 ．
相关试题
某校举行了自贡市创建全国文明城市知识竞赛活动，初一年级全体同学参加了知识竞赛．
收集教据：现随机抽取了初一年级30名同学的“创文知识竞赛”成绩，分数如下（单位：分）
90 85 68 92 81 84 95 93 87 89 78 99 89 85 97
88 81 95 86 98 95 93 89 86 84 87 79 85 89 82
整理分析数据：
|
成绩 （单位：分） |
频数（人数） |
|
|
1 |
|
|
2 |
|
|
17 |
|
|
|
（1）请将图表中空缺的部分补充完整；
（2）学校决定表彰“创文知识竞赛”成绩在90分及其以上的同学．根据上面统计结果估计该校初一年级360人中，约有多少人将获得表彰；
（3）“创文知识竞赛”中，受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章，她从中选取两枚送给弟弟，则小红送给弟弟的两枚纪念章中，恰好有恐龙图案的概率是 ．
推荐套卷
粤公网安备 44130202000953号