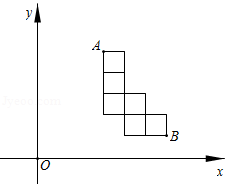初中数学中心对称图形填空题

正五边形的内角和等于______度．

如图，已知∠1=∠2，请你添加一个条件：______   _____，使△ABD≌△ACD。

（11·佛山）如图物体从点A出发，按照A→B（第1步）→C（第2）→D→A
→E→F→G→A→B→……的顺序循环运动，则第2011步到达点     
   处；

将一块直角三角形纸片ABC折叠，使点A与点C重合，展开后平铺在桌面上（如
图所示）．若∠C＝90°，BC＝8cm，则折痕DE的长度是   cm．

 

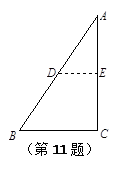下列四种说法：
①若一个三角形三个内角的度数比为2∶3∶4，则这个三角形是锐角三角形；
②“掷两枚质地均匀的正方体骰子点数之和一定大于6”是必然事件；
③购买一张彩票可能中奖；
④已知等腰三角形的一个内角为40°，则这个等腰三角形的顶角为100°其中正确的序号是．

从“线段，等边三角形，圆，矩形，正六边形”这五个图形中任取一个，取到既是轴对称图形又是中心对称图形的概率是　　．

如图，在一个 $4\times 4$的网格中，每个小正方形的边长为1，每个小正方形的顶点叫做格点．点 $A$在格点上，动点 $P$从 $A$点出发，先向右移动2个单位长度到达 $P_1$， $P_1$绕点 $A$逆时针旋转 $90°$到达 $P_2$， $P_2$再向下移动2个单位长度回到 $A$点， $P$点所经过的路径围成的图形是　      　图形（填“轴对称”或“中心对称”．）

从平行四边形、菱形、正五边形、圆、角中随机抽取一个图形，抽到既是中心对称图形又是轴对称图形的概率是 　　．

如图，已知菱形ABCD的两条对角线相交于点O，AC＝6cm，BD＝8cm，则菱形的高AE为     cm．

如图，直线 $a$、 $b$垂直相交于点 $O$，曲线 $C$关于点 $O$成中心对称，点 $A$的对称点是点 $A^{\text{'}}$， $\mathit{AB}\perp a$于点 $B$， $A^{\text{'}}D\perp b$于点 $D$．若 $\mathit{OB}=3$， $\mathit{OD}=2$，则阴影部分的面积之和为　　．

有五张背面完全相同的卡片，其正面分别画有等腰三角形、平行四边形、矩形、正方形、菱形，将这五张卡片背面朝上洗匀，从中随机抽取一张，卡片上的图形是中心对称图形的概率是　　．

正八边形的每一个内角都等于     °．

请写出一个是轴对称图形但一定不是中心对称图形的几何图形名称：　      　．

如图，在平面直角坐标系 $\mathit{xOy}$中，有一个由六个边长为1的正方形组成的图案，其中点 $A$， $B$的坐标分别为 $(3,5)$， $(6,1)$．若过原点的直线 $l$将这个图案分成面积相等的两部分，则直线 $l$的函数解析式为　　．

下列图形中：①圆；②等腰三角形；③正方形；④正五边形，既是轴对称图形又是中心对称图形的有　　个．