四川省安岳县七年级第二学期期末教学质量监测数学
一件工作,甲独做a小时完成,乙独做b小时完成,则甲乙两人合作完成需要的时间为(单位:小时)……………………………………………………( )
A. |
B. |
C.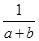 |
D.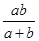 |
如图,将矩形ABCD沿DE折叠,使A点落在BC边上F处,若∠EFB=70°,则∠AED=…( )
| A.80° | B.75° | C.70° | D.65° |
如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠B=60º,BC=3,△ABE的周长为6,
则等腰梯形的周长是 ……………………………………………………( )

| A.8 | B.10 | C.12 | D.16 |
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为…( )。
| A.4 | B.6 | C.16 | D.55 |
已知任意直线l把□ABCD分成两部分,要使这两部分的面积相等,直线l所在位
置需满足的条件是 _____ ____ 。
学校规定:学生期末总评成绩由卷面成绩、研究性学习成绩、平日成绩三部分构
成,各部分所占比例如图所示,李明本学期数学学科三部分的成绩分别是90分、80分、85
分,则小明的期末数学总评成绩为 。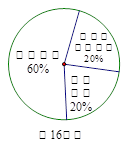
一个反比例函数在第二象限的图象如右图所示,点A是图象上任意一点,
AM⊥x轴,垂足为M,O是原点,如果△AOM的面积为3,那么这个反比例函数的解析式
是y= 。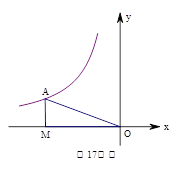
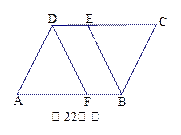
如图,观察图中菱形的个数:图1中有1个菱形,图2中有5个菱形,图3中有14个菱形,图4中有30个菱形……,则第6个图中菱形的个数是 个.
(本题共2小题,满分8分,每小题4分)
(1)先化简,再求值:  ,其中x = 2
,其中x = 2
(2)某学习小组共8人,在一次数学测验中,成绩(单位:分)分别为:
100、74、90、74、74、90、74、64,试求这个小组的平均成绩。
请你阅读下列计算过程,再回答所提出的问题:题目计算: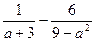
解:原式=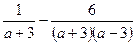
| A. = 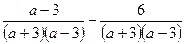 |
B. =a-3-6 |
C. =a-9 |
D. (1)上述计算过程中,从哪一步开始出现错误:_______________ 。 (2)从B到C是否正确,若不正确,错误的原因是__________________________ 。 (3)请你把正确解答过程写下来。 |
如图,在梯形ABCD中,AD∥BC,BD=CD,AB<CD,且∠ABC为
锐角,AD=4,BC=12,点E为BC上一动点。试求:当CE为何值时,四边形ABED是等腰梯
形?
每年3月12日为“植树节”,某中学积极响应“植树造林”活动的号召,组织团员植树300棵。实际参加植树的团员人数是原计划的1.5倍,这样实际人均植树棵数比原计划的少2棵,求原计划参加植树的团员有多少人?
某学校为丰富课间自由活动的内容,随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么”,整理收集到的数据,绘制成下图8所示,请根据有关信息回答下列问题:
⑴学校采用的调查方式是___ ___;
⑵求喜欢“踢毽子”的学生人数,并中图8中将“踢毽子”部分的图形补充完整;
⑶该校共有800名学生,请估计喜欢“跳绳”的学生人数.
如图1,已知反比例函数y=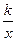 过点P, P点的坐标为(3-m,
过点P, P点的坐标为(3-m,
2m),m是分式方程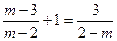 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.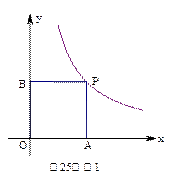
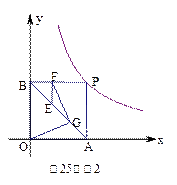
(1)求m值
(2)试判断四边形PAOB的形状,并说明理由.
(2)如图2,连结AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连结OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明.
2.下列命题中正确的有( ).
①相等的角是对顶角; ②若a//b,b//c,则a∥c;
③同位角相等; ④邻补角的平分线互相垂直.
| A.0个 | B.1个 | C.2个 | D.3个 |
如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
| A.72° | B.108° | C.144° | D.216° |

下列方程中变形正确的是( )
① 4x+8=0变形为x+2=0; ② x+6=5-2x变形为3x=-1;
③  =3变形为4x=15; ④ 4x=2变形为x=2
=3变形为4x=15; ④ 4x=2变形为x=2
| A.①④ | B.①②③ | C.③④ | D.①②④ |
在下列对称图形中,对称轴的条数最少的图形是( )
| A. | B.等边三角形 | C.正方形 | D.正六边形 |
下列正多边形的组合中,能够铺满地面的是( )
| A.正六边形和正方形 | B.正五边形和正八边形 |
| C.正六边形和正三角形 | D.正十边形和正三角形 |
小华在做解方程作业时,不小心将方程中的一个常数弄脏了而看不清楚,被弄脏
的方程是 ( -
( -  +x)=1-
+x)=1- ,这该怎么办呢?他想了一想,然后看了一下书后面
,这该怎么办呢?他想了一想,然后看了一下书后面
的答案,知道此方程的解是x=5,于是,他很快便补好了这个常数,并迅速地做完了作业。
同学们,你能补出这个常数吗?它应该是( )
| A.2 | B.3 | C.4 | D.5 |
已知代数式 xa-1y3与-5x-by2a+b是同类项,则a与b的值分别是( )
xa-1y3与-5x-by2a+b是同类项,则a与b的值分别是( )
A. |
B. |
C. |
D. |
已知 是二元一次方程组
是二元一次方程组 的解,则(2m-n)2=( )
的解,则(2m-n)2=( )
| A.4 | B.2 | C.16 | D.2或-2 |
已知等腰三角形的两边长是5和12,则它的周长是( )
| A.22 | B.29 | C.22或29 | D.17 |
一个多边形的内角和与它的一个外角和为570°,则这个多边形的边数为( )
| A.5 | B.6 | C.7 | D.8 |
若不等式组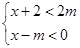 的解集为x<2m-2,则m的取值范围是( )
的解集为x<2m-2,则m的取值范围是( )
| A.m≤2 | B.m≥2 | C.m>2 | D.m<2 |
某单位购买35张电影票共用250元,其中甲种票每张8元,乙种票每张6元,则购买甲、乙两种票的数量分别为 .
下列四种说法:
①若一个三角形三个内角的度数比为2∶3∶4,则这个三角形是锐角三角形;
②“掷两枚质地均匀的正方体骰子点数之和一定大于6”是必然事件;
③购买一张彩票可能中奖;
④已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为100°其中正确的序号是.
一次数学竞赛,共有20道选择题,评分标准是:每答对1题得5分,答错1题倒扣2分,不答得0分。小英有1道题没有答,则她至少答对 道题,成绩才能在70分以上.
(本小题满分7分,其中(1)小题3分,(2)小题4分)
解下列二元一次方程组:
(1)
(2)
(本小题满分8分)小敏和小兰都想当节目主持人,但现在名额只有1个,为了能够选出1人参加,小丽想了一个办法:在三张卡片上分别写着3、-4、4,放入盒子里搅匀,随机抽取2张,若两张卡片上的数字之和为0,小敏当主持人,否则小兰当主持人,你认为这个游戏公平吗?用数据说明你的观点.
(本小题满分8分。其中(1)小题6分,(2)小题2分)
如图2:在等边三角形△ABC中,BD平分∠ABC,延长BC到E,使CE=CD,连接D、E.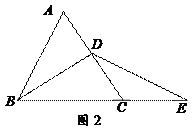
(1)小明同学说:“BD=DE”,他说得对吗?请你说明理由;
(2)小强同学说把“BD平分∠ABC”改成其它条件,也能得到同样的结论,你认为该如何改呢?
(本小题满分8分。其中(1)小题4分,(2)小题4分)
如图3:在正方形网格上有一个△ABC.
(1)作出△ABC关于直线MN的对称图形;
(2)若网格上最小正方形的边长为1,求△ABC的面积.
(本小题满分8分)列方程解应用题:
现加工一批机器零件,甲单独完成需4天,乙单独完成需6天。现由乙先做1天,然后两人合做,完成后共得报酬600元。若按个人完成的工作量给付报酬,你应如何分配呢?
(本小题满分9分,其中(1)小题5分,(2)小题4分)
如图4:在△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,点E是BC上一个动点(点E与B、C不重合),连接A、E.若a、b满足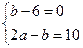 ,且c是不等式组
,且c是不等式组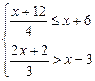 的最大整数解.
的最大整数解.
(1)求a、b、c的长.
(2)若AE平分△ABC的周长,求∠BEA的大小.
 的图象经过点
的图象经过点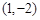 ,则函数
,则函数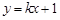 的图象不经过……( )
的图象不经过……( )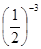 = 。
= 。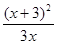 为负数,则x 。
为负数,则x 。 ;②
;② ;③
;③ ;④
;④ (a为常数,且
(a为常数,且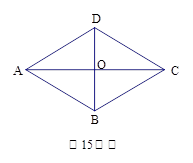

 只有5个整数解,则a的取值范围是( )
只有5个整数解,则a的取值范围是( )
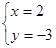 的二元一次方程组是 .
的二元一次方程组是 .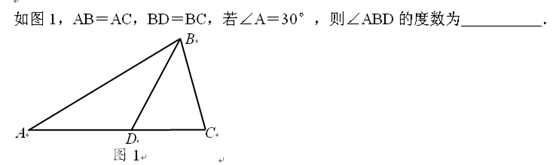
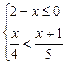 ,并将它的解集在数轴上标出来.
,并将它的解集在数轴上标出来.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号