图3.1、图3.2、图3.3均是单位为1的方格图.
(1)请把方格图3.1中的带阴影的图形适当剪开,重新拼成正方形;(画出分割线,在图3.2中画出拼成正方形的草图)
(2)所拼成正方形的边长为多少?周长为多少?
(3)利用这个事实,在图3.3的数轴上画出表示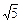 的点A.(要求保留画图痕迹)
的点A.(要求保留画图痕迹)
(4)在图3.3的数轴上画出表示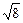 的点B.(要求保留画图痕迹)
的点B.(要求保留画图痕迹)
相关知识点
推荐套卷
图3.1、图3.2、图3.3均是单位为1的方格图.
(1)请把方格图3.1中的带阴影的图形适当剪开,重新拼成正方形;(画出分割线,在图3.2中画出拼成正方形的草图)
(2)所拼成正方形的边长为多少?周长为多少?
(3)利用这个事实,在图3.3的数轴上画出表示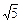 的点A.(要求保留画图痕迹)
的点A.(要求保留画图痕迹)
(4)在图3.3的数轴上画出表示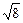 的点B.(要求保留画图痕迹)
的点B.(要求保留画图痕迹)