(9分) 如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,
BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M。
(1)求证:MB=MD,ME=MF
(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由。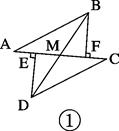

相关知识点
推荐套卷
(9分) 如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,
BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M。
(1)求证:MB=MD,ME=MF
(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由。
