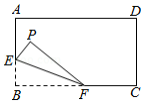
如图,在 中, , , , 、 分别是斜边 、直角边 上的点,把 沿着直线 折叠.

(1)如图1,当折叠后点 和点 重合时,用直尺和圆规作出直线 ;(不写作法和证明,保留作图痕迹)
(2)如图2,当折叠后点 落在 边上点 处,且四边形 是菱形时,求折痕 的长.
对给定的一张矩形纸片 进行如下操作:先沿 折叠,使点 落在 边上(如图① ,再沿 折叠,这时发现点 恰好与点 重合(如图②
(1)根据以上操作和发现,求 的值;
(2)将该矩形纸片展开.
①如图③,折叠该矩形纸片,使点 与点 重合,折痕与 相交于点 ,再将该矩形纸片展开.求证: ;
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的 点,要求只有一条折痕,且点 在折痕上,请简要说明折叠方法.(不需说明理由)

矩形 中, , .将矩形折叠,使点 落在点 处,折痕为 .
(1)如图①,若点 恰好在边 上,连接 ,求 的值;
(2)如图②,若 是 的中点, 的延长线交 于点 ,求 的长.

如图,矩形 中, , , 是 上一点,且 , 是 上一动点,若将 沿 对折后,点 落在点 处,则点 到点 的最短距离为 .
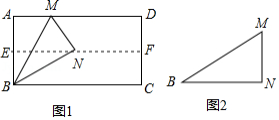
实验探究:
(1)如图1,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开;再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 , .请你观察图1,猜想 的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片 剪下,如图2.折叠该纸片,探究 与 的数量关系.写出折叠方案,并结合方案证明你的结论.
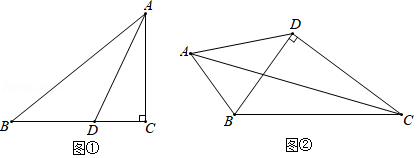
如果三角形的两个内角 与 满足 ,那么我们称这样的三角形为“准互余三角形”.
(1)若 是“准互余三角形”, , ,则 ;
(2)如图①,在 中, , , .若 是 的平分线,不难证明 是“准互余三角形”.试问在边 上是否存在点 (异于点 ,使得 也是“准互余三角形”?若存在,请求出 的长;若不存在,请说明理由.
(3)如图②,在四边形 中, , , , ,且 是“准互余三角形”,求对角线 的长.
在 中, 是 边上的一点,连接 .将 沿 翻折,使点 落在点 处,当 时,求证:四边形 是菱形.

如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.
(1)求⊙O的半径;
(2)点E为圆上一点,∠ECD=15°,将 沿弦CE翻折,交CD于点F,求图中阴影部分的面积.

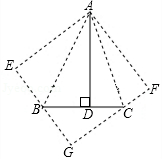
如图,在△ ABC中,∠ BAC=45°, AD⊥ BC于点 D, BD=6, DC=4,求 AD的长.小明同学利用翻折,巧妙地解答了此题,按小明的思路探究并解答下列问题:
(1)分别以 AB, AC所在直线为对称轴,画出△ ABD和△ ACD的对称图形,点 D的对称点分别为点 E, F,延长 EB和 FC相交于点 G,求证:四边形 AEGF是正方形;
(2)设 AD= x,建立关于 x的方程模型,求出 AD的长.
如图,在矩形 中, ,点 是 边上的一点,将 沿着 折叠,点 刚好落在 边上点 处;点 在 上,将 沿着 折叠,点 刚好落在 上点 处,此时 ,
(1)求证: ;
(2)求 的长;
(3)求 的值.

如图,在平面直角坐标系中,已知点 , 和 ,请按下列要求画图并填空.
(1)平移线段 ,使点 平移到点 ,画出平移后所得的线段 ,并写出点 的坐标为 ;
(2)将线段 绕点 逆时针旋转 ,画出旋转后所得的线段 ,并直接写出 的值为 ;
(3)在 轴上找出点 ,使 的周长最小,并直接写出点 的坐标为 .

如图,矩形 ABCD中, AB> AD,把矩形沿对角线 AC所在直线折叠,使点 B落在点 E处, AE交 CD于点 F,连接 DE.
(1)求证:△ ADE≌△ CED;
(2)求证:△ DEF是等腰三角形.
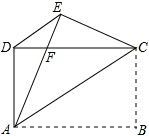
如图,将矩形ABCD沿AF折叠,使点D落在BC边上的点E处,过点E作 交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若 , ,求BE的长.

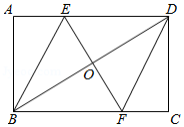
如图,四边形 是矩形, 、 分别是线段 、 上的点,点 是 与 的交点.若将 沿直线 折叠,则点 与点 重合.
(1)求证:四边形 是菱形;
(2)若 , ,求 的值.