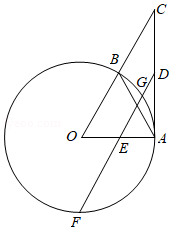
如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D, ,求 的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.

如图, 在 中, ,以 为直径作 交 于点 , 为 的中点, 连接 并延长交 的延长线于点 .
(1) 求证: 是 的切线;
(2) 若 , ,求 直径的长 .

如图,在 中, , 是 上一点,过 , , 三点的 交 于点 ,连接 , ,点 是线段 上的一点,连接 ,其中 .
(1)求证: 是 的切线.
(2)若 是 的中点, , ,求 的长.

如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且 .
(1)求证:直线MN是⊙O的切线;
(2)若 , ,求⊙O的半径.

如图,四边形 内接于 , 为 的直径, 为 的中点,过点 作 ,交 的延长线于点 .
(1)判断 与 的位置关系,并说明理由;
(2)若 的半径为5, ,求 的长.

如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且 ,延长AD到E,且有 .
(1)求证:BE是⊙O的切线;
(2)若 , ,求圆的直径AD及切线BE的长.
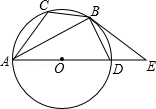
如图,在Rt△ ABC中,∠ C=90°, AD平分∠ BAC,交 BC于点 D,点 O在 AB上,⊙ O经过 A、 D两点,交 AC于点 E,交 AB于点 F.
(1)求证: BC是⊙ O的切线;
(2)若⊙ O的半径是2 cm, E是 的中点,求阴影部分的面积.(结果保留π和根号)

如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知 .
(1)求证:①直线AB是⊙O的切线;② ;
(2)求CD的长.

如图,四边形 中,连接 , ,以 为直径的 过点 ,交 于点 ,过点 作 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.(结果保留

如图,在△ ABC中,∠ C=90°, D、 F是 AB边上两点,以 DF为直径的⊙ O与 BC相交于点 E,连接 EF,∠ OFE= ∠ A.过点 F作 FG⊥ BC于点 G,交⊙ O于点 H,连接 EH.
(1)求证: BC是⊙ O的切线;
(2)连接 ED,过点 E作 EQ⊥ AB,垂足为 Q,△ EQD和△ EGH全等吗?若全等,请予以证明;若不全等,请说明理由;
(3)当 BO=5, BE=4时,求△ EHG的面积.

如图,点 A是直线 AM与⊙ O的交点,点 B在⊙ O上, BD⊥ AM垂足为 D, BD与⊙ O交于点 C, OC平分∠ AOB,∠ B=60°.
(1)求证: AM是⊙ O的切线;
(2)若 DC=2,求图中阴影部分的面积(结果保留π和根号).

如图,四边形 ABCD中, AB= AD= CD,以 AB为直径的⊙ O经过点 C,连接 AC、 OD交于点 E.
(1)证明: OD∥ BC;
(2)若tan∠ ABC=2,证明: DA与⊙ O相切;
(3)在(2)条件下,连接 BD交⊙ O于点 F,连接 EF,若 BC=1,求 EF的长.
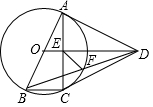
如图, 为 的直径, 为 上一点, ,延长 至点 ,使得 ,过点 作 ,垂足 在 的延长线上,连接 .
(1)求证: 是 的切线;
(2)当 时,求图中阴影部分的面积.

如图, , 是 上两点,且 ,连接 并延长到点 ,使 ,连接 .
(1)求证: 是 的切线;
(2)点 , 分别是 , 的中点, 所在直线交 于点 , , ,求 的长.