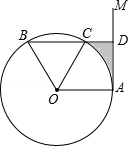
如图，点 A是直线 AM与⊙ O的交点，点 B在⊙ O上， BD⊥ AM垂足为 D， BD与⊙ O交于点 C， OC平分∠ AOB，∠ B＝60°．
（1）求证： AM是⊙ O的切线；
（2）若 DC＝2，求图中阴影部分的面积（结果保留π和根号）．
相关试题
的解集是
，求不等式
的解集。
为何值时，关于x的方程
的解是
的解的2倍。
；②
；②
推荐套卷
如图，点 A是直线 AM与⊙ O的交点，点 B在⊙ O上， BD⊥ AM垂足为 D， BD与⊙ O交于点 C， OC平分∠ AOB，∠ B＝60°．
（1）求证： AM是⊙ O的切线；
（2）若 DC＝2，求图中阴影部分的面积（结果保留π和根号）．
粤公网安备 44130202000953号