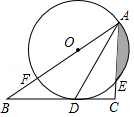
如图,在Rt△ ABC中,∠ C=90°, AD平分∠ BAC,交 BC于点 D,点 O在 AB上,⊙ O经过 A、 D两点,交 AC于点 E,交 AB于点 F.
(1)求证: BC是⊙ O的切线;
(2)若⊙ O的半径是2 cm, E是 的中点,求阴影部分的面积.(结果保留π和根号)
相关知识点
推荐套卷
如图,在Rt△ ABC中,∠ C=90°, AD平分∠ BAC,交 BC于点 D,点 O在 AB上,⊙ O经过 A、 D两点,交 AC于点 E,交 AB于点 F.
(1)求证: BC是⊙ O的切线;
(2)若⊙ O的半径是2 cm, E是 的中点,求阴影部分的面积.(结果保留π和根号)
