如图，四边形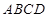
、
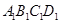是两个边长分别为5和1且中心重合的正方形．其中，正方形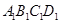可以绕中心
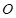旋转,正方形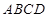静止不动．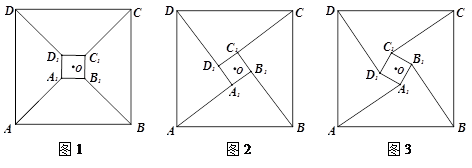
（1）如图1，当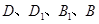
四点共线时，四边形
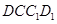的面积为__；
（2）如图2，当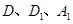
三点共线时，请直接写出
= _________；
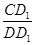（3）在正方形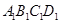绕中心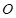旋转的过程中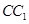，直线
与直线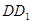
的位置关系______________,请借助图3证明你的猜想．
相关知识点
推荐套卷
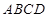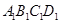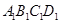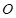如图，四边形、是两个边长分别为5和1且中心重合的正方形．其中，正方形可以绕中心旋转,正方形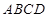静止不动．
（1）如图1，当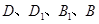四点共线时，四边形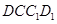的面积为__；
（2）如图2，当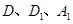三点共线时，请直接写出= _________；
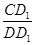（3）在正方形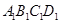绕中心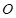旋转的过程中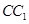，直线与直线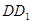的位置关系______________,请借助图3证明你的猜想．
粤公网安备 44130202000953号