已知是
的直径,弦
与
相交,
,
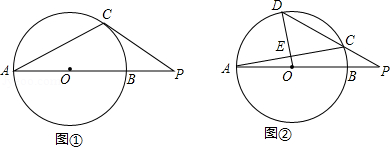
如图①,若
为
的中点,求
和
的大小;
(Ⅱ)如图②,过点作
的切线,与
的延长线交于点
,若
,求
的大小.

已知是
的直径,
是
的切线,
,
交
于点
,
是
上一点,延长
交
于点
.
(1)如图①,求和
的大小;
(2)如图②,当时,求
的大小.

在 中, 为直径, 为 上一点.
(Ⅰ)如图1.过点 作 的切线,与 的延长线相交于点 ,若 ,求 的大小;
(Ⅱ)如图2, 为 上一点,且 经过 的中点 ,连接 并延长,与 的延长线相交于点 ,若 ,求 的大小.
阅读以下材料,并按要求完成相应的任务:
莱昂哈德欧拉
是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面就是欧拉发现的一个定理:在
中,
和
分别为外接圆和内切圆的半径,
和
分别为其中外心和内心,则
.

如图1,和
分别是
的外接圆和内切圆,
与
相切分于点
,设
的半径为
,
的半径为
,外心
(三角形三边垂直平分线的交点)与内心
(三角形三条角平分线的交点)之间的距离
,则有
.
下面是该定理的证明过程(部分)
延长交
于点
,过点
作
的直径
,连接
,
.
,
(同弧所对的圆周角相等).
.
,
,①
如图2,在图1(隐去,
的基础上作
的直径
,连接
,
,
,
.
是
的直径,所以
.
与
相切于点
,所以
,
.
(同弧所对的圆周角相等),
,
.
②
任务:(1)观察发现:,
(用含
,
的代数式表示);
(2)请判断和
的数量关系,并说明理由.
(3)请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;
(4)应用:若的外接圆的半径为
,内切圆的半径为
,则
的外心与内心之间的距离为
.
如图,内接于
,且
为
的直径,
,与
交于点
,与过点
的
的切线交于点
.
(1)若,
,求
的长.
(2)试判断与
的数量关系,并说明理由.

如图是某商品的标志图案, 与 是 的两条直径,首尾顺次连接点 , , , ,得到四边形 .若 , ,则图中阴影部分的面积为

| A. |
|
B. |
|
C. |
|
D. |
|
已知的直径
,弦
与弦
交于点
.且
,垂足为点
.

(1)如图1,如果,求弦
的长;
(2)如图2,如果为弦
的中点,求
的余切值;
(3)联结、
、
,如果
是
的内接正
边形的一边,
是
的内接正
边形的一边,求
的面积.
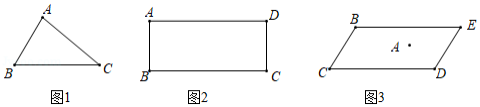
问题提出:
(1)如图1,已知,试确定一点
,使得以
,
,
,
为顶点的四边形为平行四边形,请画出这个平行四边形;
问题探究:
(2)如图2,在矩形中,
,
,若要在该矩形中作出一个面积最大的
,且使
,求满足条件的点
到点
的距离;
问题解决:
(3)如图3,有一座塔,按规定,要以塔
为对称中心,建一个面积尽可能大的形状为平行四边形的景区
.根据实际情况,要求顶点
是定点,点
到塔
的距离为50米,
,那么,是否可以建一个满足要求的面积最大的平行四边形景区
?若可以,求出满足要求的平行四边形
的最大面积;若不可以,请说明理由.(塔
的占地面积忽略不计)
如图,是
的直径,
是
的一条弦,
是
的切线.作
并与
交于点
,延长
交
于点
,交
于点
,连接
.
(1)求证:;
(2)若的半径
,
,求
的长.

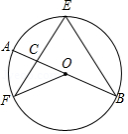
如图, 是 的直径, , 是 的弦,且 , 与 交于点 ,连接 ,若 ,则 的度数是
| A. |
|
B. |
|
C. |
|
D. |
|
问题提出
(1)如图①,已知直线及
外一点
,试在直线
上确定
、
两点,使
,并画出这个
.
问题探究
(2)如图②,是边长为28的正方形
的对称中心,
是
边上的中点,连接
.试在正方形
的边上确定点
,使线段
和
将正方形
分割成面积之比为
的两部分.求点
到点
的距离.
问题解决
(3)如图③,有一个矩形花园,
,
.根据设计要求,点
、
在对角线
上,且
,并在四边形区域
内种植一种红色花卉,在矩形内其他区域均种植一种黄色花卉.已知种植这种红色花卉每平方米需210元,种植这种黄色花卉每平方米需180元.试求按设计要求,完成这两种花卉的种植至少需费用多少元?(结果保留整数.参考数据:
,

如图,的半径
,过点
作
的切线
,且
,连接
并延长,与
交于点
、
,过点
作
,并与
交于点
,连接
、
.
(1)求证:;
(2)求的长.

如图, 的半径为5, 内接于 ,且 , ,点 在 上.若 ,则 的长为

| A. |
5 |
B. |
6 |
C. |
7 |
D. |
8 |
如图,在中,
,以斜边
上的中线
为直径作
,分别与
、
交于点
、
.
(1)过点作
的切线
与
相交于点
,求证:
;
(2)连接,求证:
.
