如图,在中,
,
是
的外接圆,点
在
上,且
,过点
作
的垂线,与
的延长线相交于点
,并与
的延长线相交于点
.
(1)求证:是
的切线;
(2)若的半径
,
,求
的长.

如图,四边形 是 的内接四边形, .若 , ,则下列等式成立的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知的半径为5,
是
的一条切线,切点为
,连接
并延长,交
于点
,过点
作
交
于点
、交
于点
,连接
,当
时,
(1)求弦的长;
(2)求证:.

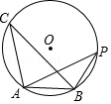
如图, 是 的内接三角形, , 的半径为5,若点 是 上的一点,在 中, ,则 的长为
| A. |
5 |
B. |
|
C. |
|
D. |
|
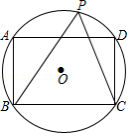
如图,矩形 内接于 ,点 是 上一点,连接 、 .若 ,则 的值为
| A. |
|
B. |
|
C. |
|
D. |
|
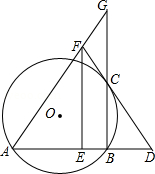
如图, 已知: 是 的弦, 过点 作 交 于点 ,过点 作 的切线交 的延长线于点 ,取 的中点 ,过点 作 交 的延长线于点 ,连接 并延长交 的延长线于点 .
求证:
(1) ;
(2) .
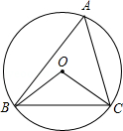
如图, 的半径为4, 是 的内接三角形,连接 、 .若 与 互补,则弦 的长为
| A. |
|
B. |
|
C. |
|
D. |
|
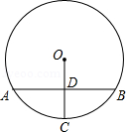
如图,在 中,弦 垂直平分半径 ,垂足为 ,若点 是 上异于点 、 的任意一点,则
| A. |
或 |
B. |
或 |
C. |
或 |
D. |
或 |
如图1,为半圆的直径,点
为圆心,
为半圆的切线,过半圆上的点
作
交
于点
,连接
.
(1)连接,若
,求证:
是半圆的切线;
(2)如图2,当线段与半圆交于点
时,连接
,
,判断
和
的数量关系,并证明你的结论.

在中,
,点
在以
为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中作弦,使
;
(2)在图2中以为边作一个
的圆周角.

如图,在中,
,
,以
为直径的半圆
交
于点
,点
是
上不与点
,
重合的任意一点,连接
交
于点
,连接
并延长交
于点
.
(1)求证:;
(2)填空:
①若,且点
是
的中点,则
的长为 ;
②取的中点
,当
的度数为 时,四边形
为菱形.

如图,在中,
,以
为直径的
交
边于点
,过点
作
,与过点
的切线交于点
,连接
.
(1)求证:;
(2)若,
,求
的长.

如图,为半圆
的直径,点
为半圆上任一点.
(1)若,过点
作半圆
的切线交直线
于点
.求证:
;
(2)若,过点
作
的平行线交半圆
于点
.当以点
,
,
,
为顶点的四边形为菱形时,求
的长.

如图,在中,
,点
为
的中点,延长
到点
,使
,
交
于点
.
(1)求证:是
的切线;
(2)若,求弦
的长.
