如图,是
的内接三角形,且
是
的直径,点
为
上的动点,且
,
的半径为6,则点
到
距离的最大值是 .

如图, , 分别是 的直径和弦, 于点 ,连接 , ,且 , ,则 的长为

| A. |
|
B. |
4 |
C. |
|
D. |
4.8 |
如图,在中,
,
,
,
平分
,
交
于点
,
交
于点
,
的外接圆
交
于点
,连接
.
(1)求证:是
的切线;
(2)求的半径
及
的正切值.
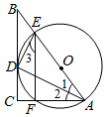
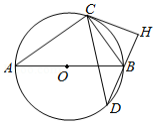
如图,为
的直径,
为
上的一点,
,
,
的延长线交
于点
,连接
.
(1)求证:是
的切线;
(2)若为
的中点,求
的值.

如图,正五边形 内接于 , 为 上的一点(点 不与点 重合),则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,为
的直径,
为
上的一点,
,
,
的延长线交
于点
,连接
.
(1)求证:是
的切线;
(2)若为
的中点,求
的值.
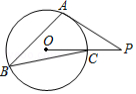
如图,已知 上三点 , , ,半径 , ,切线 交 延长线于点 ,则 的长为
| A. |
2 |
B. |
|
C. |
|
D. |
|
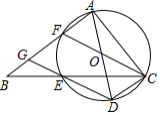
如图,在中,
,点
在
边上,且
,过
,
,
三点的
交
于另一点
,作直径
,连结
并延长交
于点
,连结
,
.
(1)求证:四边形是平行四边形.
(2)当,
时,求
的直径长.
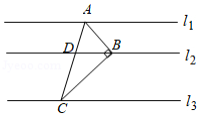
如图,直线,
,
,
分别为直线
,
,
上的动点,连接
,
,
,线段
交直线
于点
.设直线
,
之间的距离为
,直线
,
之间的距离为
,若
,
,且
,则
的最大值为 .
在屏幕上有如下内容:
如图,内接于
,直径
的长为2,过点
的切线交
的延长线于点
.张老师要求添加条件后,编制一道题目,并解答.
(1)在屏幕内容中添加条件,求
的长.请你解答.
(2)以下是小明、小聪的对话:
小明:我加的条件是,就可以求出
的长
小聪:你这样太简单了,我加的是,连结
,就可以证明
与
全等.
参考此对话,在屏幕内容中添加条件,编制一道题目(可以添线添字母),并解答.

如图1,经过等边
的顶点
,
(圆心
在
内),分别与
,
的延长线交于点
,
,连结
,
交
于点
.
(1)求证:.
(2)当,
时,求
的长.
(3)设,
.
①求关于
的函数表达式;
②如图2,连结,
,若
的面积是
面积的10倍,求
的值.

如图,已知 上三点 , , ,半径 , ,切线 交 延长线于点 ,则 的长为

| A. |
2 |
B. |
|
C. |
|
D. |
|