阅读理解:在平面直角坐标系中,若两点 、 的坐标分别是 , 、
, ,则 、 这两点间的距离为 .如 , ,则 .
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
解决问题:如图,已知在平面直角坐标系 中,直线 交 轴于点 ,点 关于 轴的对称点为点 ,过点 作直线 平行于 轴.
(1)到点 的距离等于线段 长度的点的轨迹是 ;
(2)若动点 满足到直线 的距离等于线段 的长度,求动点 轨迹的函数表达式;
问题拓展:(3)若(2)中的动点 的轨迹与直线 交于 、 两点,分别过 、 作直线 的垂线,垂足分别是 、 ,求证:
① 是 外接圆的切线;
② 为定值.
问题:已知 、 均为锐角, , ,求 的度数.
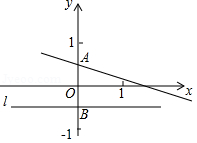
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为 ,请借助这个网格图求出 的度数;
延伸:(2)设经过图中 、 、 三点的圆弧与 交于 ,求 的弧长.

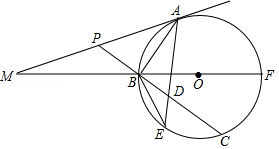
如图, 为 的直径, 为 上一点,经过点 的切线交 的延长线于点 , 交 的延长线于点 , 交 于 , 于 ,分别交 、 于 、 ,连接 , .
(1)求证: 平分 ;
(2)若 , ,
①求 的半径;
②求 的长.

如图,四边形 内接于 , 为 的直径, 与 交于点 , 为 延长线上一点,连接 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 长;
(3)在(2)的条件下,若 ,求 的面积.
定义:
数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
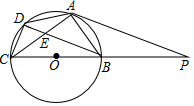
(1)如图1,已知 、 是 上两点,请在圆上找出满足条件的点 ,使 为“智慧三角形”(画出点 的位置,保留作图痕迹);
(2)如图2,在正方形 中, 是 的中点, 是 上一点,且 ,试判断 是否为“智慧三角形”,并说明理由;
运用:
(3)如图3,在平面直角坐标系 中, 的半径为1,点 是直线 上的一点,若在 上存在一点 ,使得 为“智慧三角形”,当其面积取得最小值时,直接写出此时点 的坐标.
如图,在 中, ,以 为直径的 与边 、 分别交于 、 两点,过点 作 ,垂足为点 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
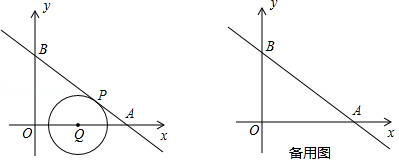
如图在平面直角坐标系中,直线 与 轴、 轴分别交于 、 两点,点 、 同时从点 出发,运动时间为 秒.其中点 沿射线 运动,速度为每秒4个单位长度,点 沿射线 运动,速度为每秒5个单位长度.以点 为圆心, 长为半径作 .
(1)求证:直线 是 的切线;
(2)过点 左侧 轴上的任意一点 ,作直线 的垂线 ,垂足为 .若 与 相切于点 ,求 与 的函数关系式(不需写出自变量的取值范围);
(3)在(2)的条件下,是否存在点 ,直线 、 、 轴与 同时相切?若存在,请直接写出此时点 的坐标;若不存在,请说明理由.
已知:如图,在 中, , 的平分线 交 于点 ,过点 作 交 于点 ,以 为直径作 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

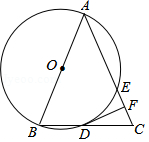
如图,已知 是 的直径, 为 上(异于 、 一点, 的切线 与 的延长线交于点 ; 为 上一点, 的延长线交 于点 , 为 上一点且 , 的延长线交 于点 .
(1)求证: ;
(2)若 、 的长是一元二次方程 的两根,求 的长;
(3)若 , ,求 的长.
(材料阅读)
地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图1中的 .人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图2所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角 的大小是变化的.
(实际应用)
观测点 在图1所示的 上,现在利用这个工具尺在点 处测得 为 ,在点 所在子午线往北的另一个观测点 ,用同样的工具尺测得 为 . 是 的直径, .
(1)求 的度数;
(2)已知
,求这两个观测点之间的距离即
上
的长.
取

在三角形纸片 (如图1)中, , .小霞用5张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图2).
(1) ;
(2)求正五边形 的边 的长.
参考值: , , .

如图, 是 的弦,过点 作 , 交 于 , .
(1)求证: 是 的切线;
(2)已知 ,点 是 上的一点.
①求 的度数;
②若 ,求 的长.

一次函数 的图象与 轴的负半轴相交于点 ,与 轴的正半轴相交于点 ,且 . 的外接圆的圆心 的横坐标为 .
(1)求一次函数的解析式;
(2)求图中阴影部分的面积.

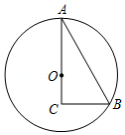
如图,在 中, , , ,以边 上一点 为圆心, 为半径的 经过点 .
(1)求 的半径;
(2)点 为劣弧 中点,作 ,垂足为 ,求 的长;
(3)在(2)的条件下,连接 ,求 的值.
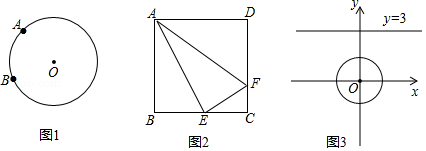
如图①,在 中, , , 是 的中点.小明对图①进行了如下探究:在线段 上任取一点 ,连接 .将线段 绕点 按逆时针方向旋转 ,点 的对应点是点 ,连接 ,得到 .小明发现,随着点 在线段 上位置的变化,点 的位置也在变化,点 可能在直线 的左侧,也可能在直线 上,还可能在直线 的右侧.
请你帮助小明继续探究,并解答下列问题:
(1)当点 在直线 上时,如图②所示.
① ;
②连接 ,直线 与直线 的位置关系是 .
(2)请在图③中画出 ,使点 在直线 的右侧,连接 .试判断直线 与直线 的位置关系,并说明理由.
(3)当点 在线段 上运动时,求 的最小值.