如图在平面直角坐标系中,直线 与 轴、 轴分别交于 、 两点,点 、 同时从点 出发,运动时间为 秒.其中点 沿射线 运动,速度为每秒4个单位长度,点 沿射线 运动,速度为每秒5个单位长度.以点 为圆心, 长为半径作 .
(1)求证:直线 是 的切线;
(2)过点 左侧 轴上的任意一点 ,作直线 的垂线 ,垂足为 .若 与 相切于点 ,求 与 的函数关系式(不需写出自变量的取值范围);
(3)在(2)的条件下,是否存在点 ,直线 、 、 轴与 同时相切?若存在,请直接写出此时点 的坐标;若不存在,请说明理由.

相关知识点
推荐套卷
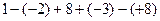 (2)
(2)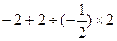
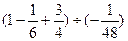 (4)
(4)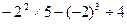
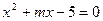 的一个根,求m的值及方程的另一根x2
的一个根,求m的值及方程的另一根x2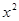 -3x-2=0
-3x-2=0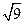 +|-2|+
+|-2|+ +(-1)2011(2)
+(-1)2011(2)
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号