初中数学全等三角形的判定与性质试题

已知：在矩形中，，分别是边，上的点，过点作的垂线交于点，以为直径作半圆．

（1）填空：点　　（填“在”或“不在” 上；当时，的值是　　；

（2）如图1，在中，当时，求证：；

（3）如图2，当的顶点是边的中点时，求证：；

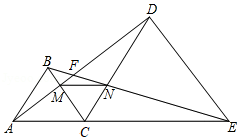
（4）如图3，点在线段的延长线上，若，连接交于点，连接，当时，，，求的值．

已知抛物线经过点和点，与轴交于另一点，顶点为．

（1）求抛物线的解析式，并写出顶点的坐标；

（2）如图，点，分别在线段，上（点不与点，重合），且，，直接写出线段的长．

如图，已知 $\mathit{AB}//\mathit{DE}$， $\mathit{AB}=\mathit{DE}$， $\mathit{BE}=\mathit{CF}$，求证： $\mathit{AC}//\mathit{DF}$．

如图，在矩形中，为对角线的中点，过点作直线分别与矩形的边，交于，两点，连接，．

（1）求证：四边形为平行四边形；

（2）若，，且，求的长．

如图，四边形 $\mathit{ABCD}$是边长为6的正方形，点 $E$在边 $\mathit{AB}$上， $\mathit{BE}=4$，过点 $E$作 $\mathit{EF}//\mathit{BC}$，分别交 $\mathit{BD}$， $\mathit{CD}$于 $G$， $F$两点．若 $M$， $N$分别是 $\mathit{DG}$， $\mathit{CE}$的中点，则 $\mathit{MN}$的长为 $($　　 $)$

A．3B． $2\sqrt{3}$C． $\sqrt{13}$D．4

如图，在中，是边上的一点，，平分，交边于点，连接．

（1）求证：；

（2）若，，求的度数．

正方形 $\mathit{ABCD}$的边长为 $6\mathit{cm}$，点 $E$、 $M$分别是线段 $\mathit{BD}$、 $\mathit{AD}$上的动点，连接 $\mathit{AE}$并延长，交边 $\mathit{BC}$于 $F$，过 $M$作 $\mathit{MN}\perp \mathit{AF}$，垂足为 $H$，交边 $\mathit{AB}$于点 $N$．

（1）如图1，若点 $M$与点 $D$重合，求证： $\mathit{AF}=\mathit{MN}$；

（2）如图2，若点 $M$从点 $D$出发，以 $1\mathit{cm}/s$的速度沿 $\mathit{DA}$向点 $A$运动，同时点 $E$从点 $B$出发，以 $\sqrt{2}\mathit{cm}/s$的速度沿 $\mathit{BD}$向点 $D$运动，运动时间为 $\mathit{ts}$．

①设 $\mathit{BF}=\mathit{ycm}$，求 $y$关于 $t$的函数表达式；

②当 $\mathit{BN}=2\mathit{AN}$时，连接 $\mathit{FN}$，求 $\mathit{FN}$的长．

如图， $E$是 $▱\mathit{ABCD}$的边 $\mathit{CD}$的中点，延长 $\mathit{AE}$交 $\mathit{BC}$的延长线于点 $F$．

（1）求证： $\mathit{\Delta ADE}\cong \mathit{\Delta FCE}$．

（2）若 $\angle \mathit{BAF}=90°$， $\mathit{BC}=5$， $\mathit{EF}=3$，求 $\mathit{CD}$的长．

如图， $E$是 $▱\mathit{ABCD}$的边 $\mathit{AD}$的中点，连接 $\mathit{CE}$并延长交 $\mathit{BA}$的延长线于 $F$，若 $\mathit{CD}=6$，求 $\mathit{BF}$的长．

如图放置的两个正方形，大正方形 $\mathit{ABCD}$边长为 $a$，小正方形 $\mathit{CEFG}$边长为 $b(a>b)$， $M$在 $\mathit{BC}$边上，且 $\mathit{BM}=b$，连接 $\mathit{AM}$， $\mathit{MF}$， $\mathit{MF}$交 $\mathit{CG}$于点 $P$，将 $\mathit{\Delta ABM}$绕点 $A$旋转至 $\mathit{\Delta ADN}$，将 $\mathit{\Delta MEF}$绕点 $F$旋转至 $\mathit{\Delta NGF}$，给出以下五个结论：① $\angle \mathit{MAD}=\angle \mathit{AND}$；② $\mathit{CP}=b-\frac{b^2}{a}$；③ $\mathit{\Delta ABM}\cong \mathit{\Delta NGF}$；④ $S_{\mathit{四边形AMFN}}=a^2+b^2$；⑤ $A$， $M$， $P$， $D$四点共圆，其中正确的个数是 $($　　 $)$

A．2B．3C．4D．5

已知：如图，在中，延长至点，延长至点，使得．连接，与对角线交于点．

求证：．

综合与实践

背景阅读 早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于我国古代著名数学著作《周髀算经》中，为了方便，在本题中，我们把三边的比为的三角形称为，4，型三角形，例如：三边长分别为9，12，15或，，的三角形就是，4，型三角形，用矩形纸片按下面的操作方法可以折出这种类型的三角形．

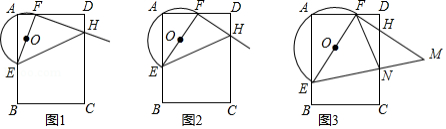
实践操作 如图1，在矩形纸片中，，．

第一步：如图2，将图1中的矩形纸片沿过点的直线折叠，使点落在上的点处，折痕为，再沿折叠，然后把纸片展平．

第二步：如图3，将图2中的矩形纸片再次折叠，使点与点重合，折痕为，然后展平，隐去．

第三步：如图4，将图3中的矩形纸片沿折叠，得到△，再沿折叠，折痕为，与折痕交于点，然后展平．

问题解决

（1）请在图2中证明四边形是正方形．

（2）请在图4中判断与的数量关系，并加以证明；

（3）请在图4中证明，4，型三角形；

探索发现

（4）在不添加字母的情况下，图4中还有哪些三角形是，4，型三角形？请找出并直接写出它们的名称．

如图，和都是等边三角形，且点、、在同一直线上，与、分别交于点、，与交于点．下列结论正确的是　　（写出所有正确结论的序号）．

①；②；③；④

已知，在如图所示的“风筝”图案中，，，．求证：．

如图①，等腰直角三角形的直角顶点为正方形的中心，点，分别在和上，现将绕点逆时针旋转角，连接，（如图②．

（1）在图②中，　　；（用含的式子表示）

（2）在图②中猜想与的数量关系，并证明你的结论．