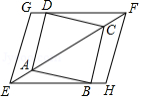
如图,在 中, ,四个角的平分线 , , , 的交点分别是 , ,过点 , 分别作 与 间的垂线 与 ,在 与 上的垂足分别是 , 与 , ,连接 .
(1)求证:四边形 是矩形;
(2)已知: , , ,求 的长.

如图,在正方形 中,分别过顶点 , 作 交对角线 所在直线于 , 点,并分别延长 , 到点 , ,使 ,连接 , .
(1)求证:四边形 是平行四边形;
(2)已知: , , ,求四边形 的周长.
如图1,在正方形 中,点 是 边上的一个动点(点 与点 , 不重合),连接 ,过点 作 于点 ,交 于点 .
(1)求证: ;
(2)如图2,当点 运动到 中点时,连接 ,求证: ;
(3)如图3,在(2)的条件下,过点 作 于点 ,分别交 , 于点 , ,求 的值.

如图, 是 的直径,弦 于点 ,点 是 上一点,且 ,连接 , , 交 于点 .
(1)若 , ,求 的半径;
(2)求证: 为等腰三角形;
(3)连接 并延长,交 的延长线于点 ,过点 作 的切线,交 的延长线于点 .求证: .

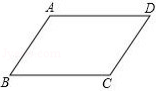
平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.
已知:如图,在四边形 中, , .
求证:四边形 是平行四边形.
证明:
已知: .
求作: ,使得 .
作法:
①以 为圆心,任意长为半径画弧,分别交 , 于点 , ;
②画一条射线 ,以点 为圆心, 长为半径画弧,交 于点 ;
③以点 为圆心, 长为半径画弧,与第②步中所画的弧相交于点 ;
④过点 画射线 ,则 .
根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出 (请保留作图痕迹).
(2)完成下面证明 的过程(注 括号里填写推理的依据).
证明:由作法可知 , , ,
△
.

如图,在矩形 中, , 分别是 , 边上的点,且 .
(1)求证: ;
(2)当 时,四边形 是菱形吗?请说明理由.

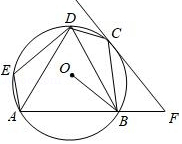
如图,五边形 内接于 , 与 相切于点 ,交 延长线于点 .
(1)若 , ,求证: ;
(2)若 , , ,求 的长.
如图,在矩形 中,以 边为直径作半圆 , 交 边于点 ,对角线 与半圆 的另一个交点为 ,连接 .
(1)求证: 是半圆 的切线;
(2)若 , ,求 的长.

如图,菱形 中,作 、 ,分别交 、 的延长线于点 、 .
(1)求证: ;
(2)若点 恰好是 的中点, ,求 的值.

如图,已知 为 的角平分线, , ,以 为圆心, 为半径的圆分别交 , 于点 , ,连接 并延长交 于点 .
(1)求证: 是 的切线;
(2)求 的值;
(3)求 的值.

如图, 在正方形 中, , 分别为 , 边上的点, , 交于点 ,且 .
(1) 求证: ;
(2) 若 , ,求正方形 的面积 .
