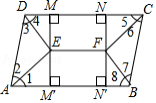
如图,在 中, ,四个角的平分线 , , , 的交点分别是 , ,过点 , 分别作 与 间的垂线 与 ,在 与 上的垂足分别是 , 与 , ,连接 .
(1)求证:四边形 是矩形;
(2)已知: , , ,求 的长.
相关知识点
推荐套卷
如图,在 中, ,四个角的平分线 , , , 的交点分别是 , ,过点 , 分别作 与 间的垂线 与 ,在 与 上的垂足分别是 , 与 , ,连接 .
(1)求证:四边形 是矩形;
(2)已知: , , ,求 的长.
