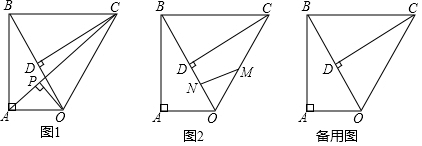
已知Rt△ OAB,∠ OAB=90°,∠ ABO=30°,斜边 OB=4,将Rt△ OAB绕点 O顺时针旋转60°,如图1,连接 BC.
(1)填空:∠ OBC= °;
(2)如图1,连接 AC,作 OP⊥ AC,垂足为 P,求 OP的长度;
(3)如图2,点 M, N同时从点 O出发,在△ OCB边上运动, M沿 O→ C→ B路径匀速运动, N沿 O→ B→ C路径匀速运动,当两点相遇时运动停止,已知点 M的运动速度为1.5单位/秒,点 N的运动速度为1单位/秒,设运动时间为 x秒,△ OMN的面积为 y,求当 x为何值时 y取得最大值?最大值为多少?
已知:如图,在菱形 中,点 、 分别在边 、 上, , 的延长线交 的延长线于点 , 的延长线交 的延长线于点 .
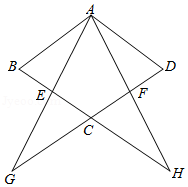
[小题1]求证: ;
[小题2]如果 ,求证: .
【问题】
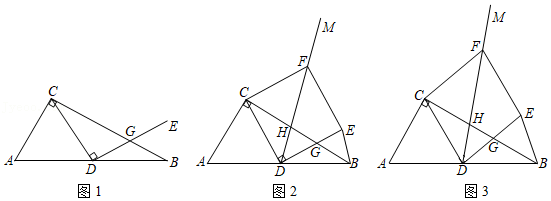
如图1,在Rt△ ABC中,∠ ACB=90°, AC= BC,过点 C作直线 l平行于 AB.∠ EDF=90°,点 D在直线 l上移动,角的一边 DE始终经过点 B,另一边 DF与 AC交于点 P,研究 DP和 DB的数量关系.
【探究发现】
(1)如图2,某数学兴趣小组运用"从特殊到一般"的数学思想,发现当点 D移动到使点 P与点 C重合时,通过推理就可以得到 DP= DB,请写出证明过程;
【数学思考】
(2)如图3,若点 P是 AC上的任意一点(不含端点 A、 C),受(1)的启发,这个小组过点 D作 DG⊥ CD交 BC于点 G,就可以证明 DP= DB,请完成证明过程;
【拓展引申】
(3)如图4,在(1)的条件下, M是 AB边上任意一点(不含端点 A、 B), N是射线 BD上一点,且 AM= BN,连接 MN与 BC交于点 Q,这个数学兴趣小组经过多次取 M点反复进行实验,发现点 M在某一位置时 BQ的值最大.若 AC= BC=4,请你直接写出 BQ的最大值.

如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .
(1)如图1,若 ,则线段 与 的数量关系是 , ;
(2)如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .
①试判断四边形 的形状,并说明理由;
②求证: ;
(3)如图3,若 , ,过点 作 交 于点 ,连接 , ,请直接写出 的值(用含 的式子表示).
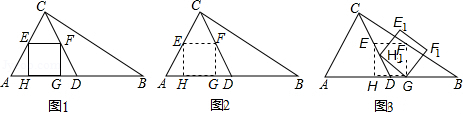
如图1,在△ ABC中,∠ ACB=90°,∠ B=30°, AC=4, D是 AB的中点, EF是△ ACD的中位线,矩形 EFGH的顶点都在△ ACD的边上.
(1)求线段 EF、 FG的长;
(2)如图2,将矩形 EFGH沿 AB向右平移,点 F落在 BC上时停止移动,设矩形移动的距离为 x,矩形与△ CBD重叠部分的面积为 S,求出 S关于 x的函数解析式;
(3)如图3,矩形 EFGH平移停止后,再绕点 G按顺时针方向旋转,当点 H落在 CD边上时停止旋转,此时矩形记作 E 1 F 1 GH 1,设旋转角为α,求cosα的值.
如图(1)放置两个全等的含有 角的直角三角板 与 ,若将三角板 向右以每秒1个单位长度的速度移动(点 与点 重合时移动终止),移动过程中始终保持点 、 、 、 在同一条直线上,如图(2), 与 、 分别交于点 、 , 与 交于点 ,其中 ,设三角板 移动时间为 秒.

(1)在移动过程中,试用含 的代数式表示 的面积;
(2)计算 等于多少时,两个三角板重叠部分的面积有最大值?最大值是多少?
如图, 和
和 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形, ,点
,点 为射线
为射线 ,
, 的交点.
的交点.
(1)求证: ;
;
(2)若 ,
, ,把
,把 绕点
绕点 旋转,
旋转,
①当 时,求
时,求 的长;
的长;
②直接写出旋转过程中线段 长的最小值与最大值.
长的最小值与最大值.

研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题.
(1)阅读材料
立体图形中既不相交也不平行的两条直线所成的角,就是将直线平移使其相交所成的角.
例如,正方体 (图 ,因为在平面 中, , 与 相交于点 ,所以直线 与 所成的 就是既不相交也不平行的两条直线 与 所成的角.
解决问题
如图1,已知正方体 ,求既不相交也不平行的两直线 与 所成角的大小.

(2)如图2, , 是正方体相邻两个面上的点;
①下列甲、乙、丙三个图形中,只有一个图形可以作为图2的展开图,这个图形是 ;
②在所选正确展开图中,若点 到 , 的距离分别是2和5,点 到 , 的距离分别是4和3, 是 上一动点,求 的最小值.

如图,将等腰直角三角形纸片 对折,折痕为 .展平后,再将点 折叠在边 上(不与 、 重合),折痕为 ,点 在 上的对应点为 ,设 与 交于点 ,连接 .已知 .
(1)若 为 的中点,求 的长;
(2)随着点 在边 上取不同的位置,
① 的形状是否发生变化?请说明理由;
②求 的周长的取值范围.

在 中, , 是边 上一动点,连接 ,将 绕点 逆时针旋转至 的位置,使得 .
(1)如图1,当 时,连接 ,交 于点 .若 平分 , ,求 的长;
(2)如图2,连接 ,取 的中点 ,连接 .猜想 与 存在的数量关系,并证明你的猜想;
(3)如图3,在(2)的条件下,连接 , .若 ,当 , 时,请直接写出 的值.

在扇形 中,半径 ,点 在 上,连结 ,将 沿 折叠得到△ .
(1)如图1,若 ,且 与 所在的圆相切于点 .
①求 的度数.
②求 的长.
(2)如图2, 与 相交于点 ,若点 为 的中点,且 ,求 的长.
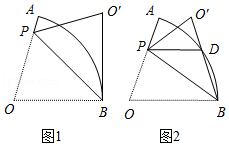
已知,在 中, , .

(1)如图1,已知点 在 边上, , ,连结 .试探究 与 的关系;
(2)如图2,已知点 在 下方, , ,连结 .若 , , , 交 于点 ,求 的长;
(3)如图3,已知点 在 下方,连结 、 、 .若 , , , ,求 的值.
在矩形 中, ,点 、 分别是边 、 上的动点,且 ,连接 ,将矩形 沿 折叠,点 落在点 处,点 落在点 处.
(1)如图1,当 与线段 交于点 时,求证: ;
(2)如图2,当点 在线段 的延长线上时, 交 于点 ,求证:点 在线段 的垂直平分线上;
(3)当 时,在点 由点 移动到 中点的过程中,计算出点 运动的路线长.
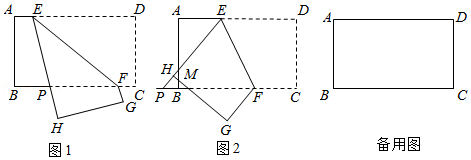
在 中, , , 是边 上一点,将 沿 折叠得到 ,连接 .
(1)特例发现
如图1,当 , 落在直线 上时.
①求证: ;
②填空: 的值为 ;
(2)类比探究
如图2,当 , 与边 相交时,在 上取一点 ,使 , 交 于点 .探究 的值(用含 的式子表示),并写出探究过程;
(3)拓展运用
在(2)的条件下,当 , 是 的中点时,若 ,求 的长.
