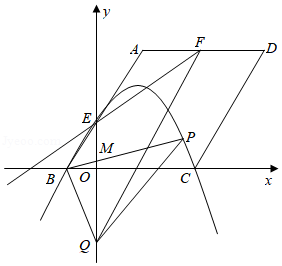
已知抛物线 的对称轴为直线 .
(1)求 的值;
(2)若点 , , , 都在此抛物线上,且 , .比较 与 的大小,并说明理由;
(3)设直线 与抛物线 交于点 、 ,与抛物线 交于点 , ,求线段 与线段 的长度之比.
如图,抛物线
的顶点为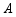 ,与
,与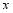 轴的正半轴交于点
轴的正半轴交于点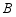 .
.
(1)将抛物线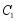 上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;
上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;
(2)将抛物线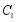 上的点
上的点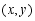 变为
变为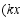 ,
, ,变换后得到的抛物线记作
,变换后得到的抛物线记作 ,抛物线
,抛物线 的顶点为
的顶点为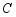 ,点
,点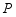 在抛物线
在抛物线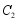 上,满足
上,满足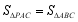 ,且
,且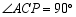 .
.
①当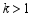 时,求
时,求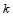 的值;
的值;
②当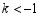 时,请直接写出
时,请直接写出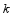 的值,不必说明理由.
的值,不必说明理由.
若两条抛物线的顶点相同,则称它们为"友好抛物线",抛物线 C 1: y 1=﹣2 x 2+4 x+2与 C 2: y 2=﹣ x 2+ mx+ n为"友好抛物线".
(1)求抛物线 C 2的解析式.
(2)点 A是抛物线 C 2上在第一象限的动点,过 A作 AQ⊥ x轴, Q为垂足,求 AQ+ OQ的最大值.
(3)设抛物线 C 2的顶点为 C,点 B的坐标为(﹣1,4),问在 C 2的对称轴上是否存在点 M,使线段 MB绕点 M逆时针旋转90°得到线段 MB′,且点 B′恰好落在抛物线 C 2上?若存在求出点 M的坐标,不存在说明理由.

阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有: , , , .

问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线 经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
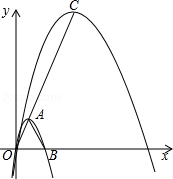
在平面直角坐标系中,已知抛物线 的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
(1)填空:b= ,c= ,直线AC的解析式为 ;
(2)直线 与x轴相交于点H.
①当 时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若 ,求出此时点D的坐标;
②当 时(如图2),直线 与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为 ,求此时t的值.

如图,直线 与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和 个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
(1)求点A,点B的坐标;
(2)用含t的代数式分别表示EF和AF的长;
(3)当四边形ADEF为菱形时,试判断△AFG与△AGB是否相似,并说明理由.
(4)是否存在t的值,使△AGF为直角三角形?若存在,求出这时抛物线的解析式;若不存在,请说明理由.

如图1,在平面直角坐标系中,点为坐标原点,抛物线
与
轴交于点
,与
轴交于点
,
.
(1)直接写出抛物线的解析式及其对称轴;
(2)如图2,连接,
,设点
是抛物线上位于第一象限内的一动点,且在对称轴右侧,过点
作
于点
,交
轴于点
,过点
作
交
于点
,交
轴于点
.设线段
的长为
,求
与
的函数关系式,并注明
的取值范围;
(3)在(2)的条件下,若的面积为
,
①求点的坐标;
②设为直线
上一动点,连接
,直线
交直线
于点
,则点
在运动过程中,在抛物线上是否存在点
,使得
为等腰直角三角形?若存在,请直接写出点
及其对应的点
的坐标;若不存在,请说明理由.
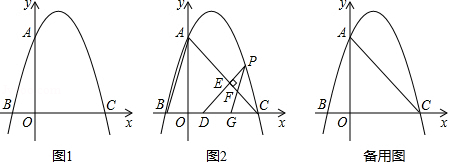
已知抛物线和
(1)如何将抛物线平移得到抛物线
?
(2)如图1,抛物线与
轴正半轴交于点
,直线
经过点
,交抛物线
于另一点
.请你在线段
上取点
,过点
作直线
轴交抛物线
于点
,连接
.
①若,求点
的横坐标;
②若,直接写出点
的横坐标.
(3)如图2,的顶点
、
在抛物线
上,点
在点
右边,两条直线
、
与抛物线
均有唯一公共点,
、
均与
轴不平行.若
的面积为2,设
、
两点的横坐标分别为
、
,求
与
的数量关系.

已知抛物线
与 轴交于点
轴交于点 ,与
,与 轴的两个交点分别为
轴的两个交点分别为 ,
, .
.
(1)求抛物线的解析式;
(2)已知点 在抛物线上,连接
在抛物线上,连接 ,
, ,若
,若 是以
是以 为直角边的直角三角形,求点
为直角边的直角三角形,求点 的坐标;
的坐标;
(3)已知点 在
在 轴上,点
轴上,点 在抛物线上,是否存在以
在抛物线上,是否存在以 ,
, ,
, ,
, 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

如图,在平面直角坐标系中,已知抛物线 y= x 2+ x﹣2与 x轴交于 A, B两点(点 A在点 B的左侧),与 y轴交于点 C,直线 l经过 A, C两点,连接 BC.
(1)求直线 l的解析式;
(2)若直线 x= m( m<0)与该抛物线在第三象限内交于点 E,与直线 l交于点 D,连接 OD.当 OD⊥ AC时,求线段 DE的长;
(3)取点 G(0,﹣1),连接 AG,在第一象限内的抛物线上,是否存在点 P,使∠ BAP=∠ BCO﹣∠ BAG?若存在,求出点 P的坐标;若不存在,请说明理由.

如图,在▱ OABC中, A、 C两点的坐标分别为(4,0)、(﹣2,3),抛物线 W经过 O、 A、 C三点,点 D是抛物线 W的顶点.

(1)求抛物线 W的函数解析式及顶点 D的坐标;
(2)将抛物线 W和▱ OABC同时先向右平移4个单位长度,再向下平移 m(0< m<3)个单位长度,得到抛物线 W 1和□ O 1 A 1 B 1 C 1,在向下平移过程中, O 1 C 1与 x轴交于点 H,▱ O 1 A 1 B 1 C 1与▱ OABC重叠部分的面积记为 S,试探究:当 m为何值时, S有最大值,并求出 S的最大值;
(3)在(2)的条件下,当 S取最大值时,设此时抛物线 W 1的顶点为 F,若点 M是 x轴上的动点,点 N是抛物线 W 1上的动点,是否存在这样的点 M、 N,使以 D、 F、 M、 N为顶点的四边形是平行四边形?若存在,求出点 M的坐标;若不存在,请说明理由.
如图,抛物线y=﹣x2+bx+c与直线AB交于A(﹣4,﹣4),B(0,4)两点,直线AC: 交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=﹣x2+bx+c的表达式;
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求 AM+CM它的最小值.

如图①,已知 的三个顶点坐标分别为 、 、 ,直线 交 轴正半轴于点 .
(1)求经过 、 、 三点的抛物线解析式及顶点 的坐标;
(2)连接 、 ,设 , ,若 ,求点 的坐标;
(3)如图②,在(2)的条件下,动点 从点 出发以每秒 个单位的速度在直线 上移动(不考虑点 与点 、 重合的情况),点 为抛物线上一点,设点 移动的时间为 秒,在点 移动的过程中,以 、 、 、 四个点为顶点的四边形能否成为平行四边形?若能,直接写出所有满足条件的 值及点 的个数;若不能,请说明理由.

如图,在平面直角坐标系 中,平行四边形 的 边与 轴交于 点, 是 的中点, 、 、 的坐标分别为 , , .
(1)求过 、 、 三点的抛物线的解析式;
(2)试判断抛物线的顶点是否在直线 上;
(3)设过 与 平行的直线交 轴于 , 是线段 之间的动点,射线 与抛物线交于另一点 ,当 的面积最大时,求 的坐标.