如图,一次函数 的图象与反比例函数 的图象交于 , 两点,与 , 轴交于 , 两点,且 , , ,作 轴于 点.
(1)求一次函数的解析式和反比例函数的解析式;
(2)求 的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量 的取值范围.

如图,已知反比例函数 的图象经过点 ,一次函数 的图象经过反比例函数图象上的点 .
(1)求反比例函数与一次函数的表达式;
(2)一次函数的图象分别与 轴、 轴交于 、 两点,与反比例函数图象的另一个交点为 点,连接 、 ,求 的面积.
当 时,函数 的图象上至少有一点在函数 的图象下方,则 的取值范围为
A. B. C. D.
如图,在平面直角坐标系中,一次函数 和 的图象相交于点 ,反比例函数 的图象经过点 .
(1)求反比例函数的表达式;
(2)设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.

如图,一次函数 与反比例函数 的图象交于 , 两点,与坐标轴分别交于 、 两点.
(1)求一次函数的解析式;
(2)根据图象直接写出 中 的取值范围;
(3)求 的面积.

如图所示,在平面直角坐标系中,一次函数 与反比例函数 的图象交于第二、四象限 、 两点,过点 作 轴于 , , ,且点 的坐标为 .
(1)求一次函数与反比例函数的解析式;
(2) 是 轴上一点,且 是等腰三角形,请直接写出所有符合条件的 点坐标.
如图,直线 与坐标轴分别交于点 , ,与双曲线 交于点 ,则 的长是

A. B. C. D.
如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交于点 ,与 轴相交于点 .
(1)求反比例函数的表达式;
(2)过点 的直线交反比例函数的图象于另一点 ,交 轴正半轴于点 ,当 是以 为底的等腰三角形时,求直线 的函数表达式及点 的坐标.
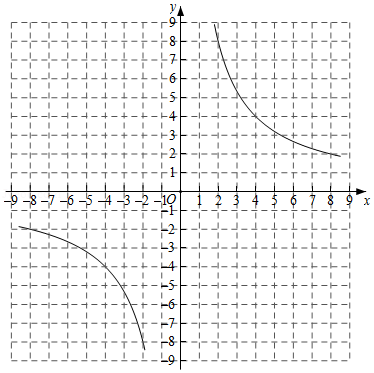
探究函数性质时,我们经历了列表、描点、连线画函数图象,观察分析图象特征,概括函数性质的过程.以下是我们研究函数 性质及其应用的部分过程,请按要求完成下列各小题.
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
6 |
5 |
4 |
|
2 |
1 |
|
7 |
|
(1)写出函数关系式中 及表格中 , 的值:
, , ;
(2)根据表格中的数据在所给的平面直角坐标系中画出该函数的图象,并根据图象写出该函数的一条性质: ;
(3)已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.
在直角坐标系中,设函数 是常数, , 与函数 是常数, 的图象交于点 ,点 关于 轴的对称点为点 .
(1)若点 的坐标为 ,
①求 , 的值;
②当 时,写出 的取值范围;
(2)若点 在函数 是常数, 的图象上,求 的值.

如图,一次函数 的图象与反比例函数 的图象交于点 、 ,与 轴交于点 ,若 ,且 .
(1)求反比例函数与一次函数的表达式;
(2)请直接写出不等式 的解集.
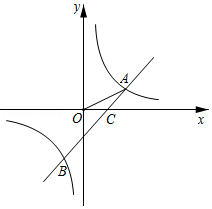
如图,一次函数 的图象与反比例函数 的图象交于 A(﹣1, n), B(3,﹣2)两点.
(1)求一次函数和反比例函数的解析式;
(2)点 P在 x轴上,且满足△ ABP的面积等于4,请直接写出点 P的坐标.

如图,在直角坐标系中,直线 与双曲线 分别相交于第二、四象限内的 , 两点,与 轴相交于 点.已知 , .
(1)求 , 对应的函数表达式;
(2)求 的面积;
(3)直接写出当 时,不等式 的解集.
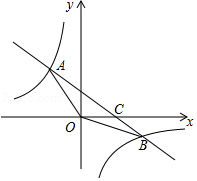
如图,在平面直角坐标系中,直线 与双曲线 交于 、 两点, 交 轴于点 ,且 .
(1)求双曲线的解析式;
(2)求点 的坐标,并直接写出 时 的取值范围.
