如图,在平面直角坐标系中,已知直线 和双曲线 ,在直线上取一点,记为 ,过 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交直线于点 ,过 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交直线于点 , ,依次进行下去,记点 的横坐标为 ,若 ,则 .

如图,在平面直角坐标系中, 的顶点坐标分别为 , , ,点 绕点 旋转 得到点 ,点 绕点 旋转 得到点 ,点 绕点 旋转 得到点 ,点 绕点 旋转 得到点 , ,按此作法进行下去,则点 的坐标为 .
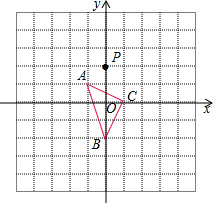
如图,正 的边长为2, 为坐标原点, 在 轴上, 在第二象限, 沿 轴正方向作无滑动的翻滚,经一次翻滚后得到△ ,则翻滚3次后点 的对应点的坐标是 ,翻滚2017次后 中点 经过的路径长为 .
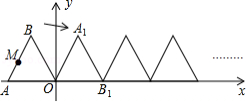
如图,在平面直角坐标系中,点 ,直线 与 轴交于点 ,以 为边作等边 ,过点 作 轴,交直线 于点 ,以 为边作等边△ ,过点 作 轴,交直线 于点 ,以 为边作等边△ ,以此类推 ,则点 的纵坐标是 .

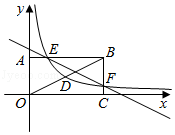
如图,在平面直角坐标系中,矩形 的两边 、 分别在坐标轴上,且 , ,连接 .反比例函数 的图象经过线段 的中点 ,并与 、 分别交于点 、 .一次函数 的图象经过 、 两点.
(1)分别求出一次函数和反比例函数的表达式;
(2)点 是 轴上一动点,当 的值最小时,点 的坐标为 .
如图,将一等边三角形的三条边各8等分,按顺时针方向(图中箭头方向)标注各等分点的序号0、1、2、3、4、5、6、7、8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点 的坐标可表示为 ,2, ,点 的坐标可表示为 ,1, ,按此方法,则点 的坐标可表示为 .

如图,一直线与两坐标轴的正半轴分别交于 , 两点, 是线段 上任意一点(不包括端点),过 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是
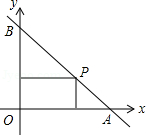
A. B. C. D.
如图1,在平面直角坐标系中, 的顶点 , 分别是直线 与坐标轴的交点,点 的坐标为 ,点 是边 上的一点, 于点 ,点 在边 上,且 , 两点关于 轴上的某点成中心对称,连结 , .设点 的横坐标为 , 为 ,请探究:
①线段 长度是否有最小值.
② 能否成为直角三角形.
小明尝试用“观察 猜想 验证 应用”的方法进行探究,请你一起来解决问题.
(1)小明利用“几何画板”软件进行观察,测量,得到 随 变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图 .请你在图2中连线,观察图象特征并猜想 与 可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出 关于 的函数表达式及自变量的取值范围,并求出线段 长度的最小值.
(3)小明通过观察,推理,发现 能成为直角三角形,请你求出当 为直角三角形时 的值.

如图,在平面直角坐标系中,正方形 的顶点 在 轴正半轴上,顶点 , 在第一象限,顶点 的坐标 , .反比例函数 (常数 , 的图象恰好经过正方形 的两个顶点,则 的值是 .

如图,在平面直角坐标系中,有一只用七巧板拼成的"猫",三角形①的边 及四边形②的边 都在 轴上,"猫"耳尖 在 轴上.若"猫"尾巴尖 的横坐标是1,则"猫"爪尖 的坐标是 .

在平面直角坐标系中,平行四边形 的对称中心是坐标原点,顶点 、 的坐标分别是 、 ,将平行四边形 沿 轴向右平移3个单位长度,则顶点 的对应点 的坐标是 .
如图,在直角坐标系中,点 , 是第一象限角平分线上的两点,点 的纵坐标为1,且 ,在 轴上取一点 ,连接 , , , ,使得四边形 的周长最小,这个最小周长的值为 .
