初中数学根的判别式解答题

已知关于 $x$的一元二次方程 $x^2-(2k+1)x+k^2+k=0$．

（1）求证：无论 $k$取何值，方程都有两个不相等的实数根．

（2）如果方程的两个实数根为 $x_1$， $x_2$，且 $k$与 $\frac{x_1}{x_2}$都为整数，求 $k$所有可能的值．

已知关于 $x$的一元二次方程 $x^2+x-m=0$．

（1）若方程有两个不相等的实数根，求 $m$的取值范围；

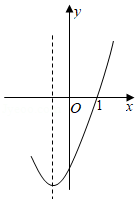
（2）二次函数 $y=x^2+x-m$的部分图象如图所示，求一元二次方程 $x^2+x-m=0$的解．

在面积都相等的所有矩形中，当其中一个矩形的一边长为1时，它的另一边长为3．

（1）设矩形的相邻两边长分别为 $x$， $y$．

①求 $y$关于 $x$的函数表达式；

②当 $y⩾3$时，求 $x$的取值范围；

（2）圆圆说其中有一个矩形的周长为6，方方说有一个矩形的周长为10，你认为圆圆和方方的说法对吗？为什么？

已知关于 $x$的一元二次方程 $x^2-2x+a=0$的两实数根 $x_1$， $x_2$满足 $x_1{x}_2+x_1+x_2>0$，求 $a$的取值范围．

已知关于 $x$的一元二次方程 $x^2-(2m-2)x+(m^2-2m)=0$．

（1）求证：方程有两个不相等的实数根．

（2）如果方程的两实数根为 $x_1$， $x_2$，且 $x_1^2+x_2^2=10$，求 $m$的值．

已知关于 $x$的一元二次方程 $m{x}^2+(1-5m)x-5=0(m\ne 0)$．

（1）求证：无论 $m$为任何非零实数，此方程总有两个实数根；

（2）若抛物线 $y=m{x}^2+(1-5m)x-5$与 $x$轴交于 $A(x_1$， $0)$、 $B(x_2$， $0)$两点，且 $|x_1-x_2|=6$，求 $m$的值；

（3）若 $m>0$，点 $P(a,b)$与 $Q(a+n,b)$在（2）中的抛物线上（点 $P$、 $Q$不重合），求代数式 $4a^2-n^2+8n$的值．

已知关于 $x$的一元二次方程 $x^2-(m-3)x-m=0$

（1）求证：方程有两个不相等的实数根；

（2）如果方程的两实根为 $x_1$、 $x_2$，且 $x_1^2+x_2^2-x_1{x}_2=7$，求 $m$的值．

如图，一次函数 $y_1=\mathit{ax}+b$与反比例函数 $y_2=\frac{4}{x}$的图象交于 $A$、 $B$两点．点 $A$的横坐标为2，点 $B$的纵坐标为1．

（1）求 $a$， $b$的值．

（2）在反比例 $y_2=\frac{4}{x}$第三象限的图象上找一点 $P$，使点 $P$到直线 $\mathit{AB}$的距离最短，求点 $P$的坐标．

已知关于 $x$的一元二次方程 $x^2-5x+2m=0$有实数根．

（1）求 $m$的取值范围；

（2）当 $m=\frac{5}{2}$时，方程的两根分别是矩形的长和宽，求该矩形外接圆的直径．

关于 $x$的方程 $2x^2-5x\sin A+2=0$有两个相等的实数根，其中 $\angle A$是锐角三角形 $\mathit{ABC}$的一个内角．

（1）求 $\sin A$的值；

（2）若关于 $y$的方程 $y^2-10y+k^2-4k+29=0$的两个根恰好是 $\mathit{\Delta ABC}$的两边长，求 $\mathit{\Delta ABC}$的周长．

已知关于 $x$的一元二次方程： $x^2-(t-1)x+t-2=0$．

（1）求证：对于任意实数 $t$，方程都有实数根；

（2）当 $t$为何值时，方程的两个根互为相反数？请说明理由．

已知关于 $x$的一元二次方程： $x^2-2x-k-2=0$有两个不相等的实数根．

（1）求 $k$的取值范围；

（2）给 $k$取一个负整数值，解这个方程．

我们规定：若 $\vec{m}=(a,b)$， $\vec{n}=(c,d)$，则 $\vec{m}·\vec{n}=\mathit{ac}+\mathit{bd}$．如 $\vec{m}=(1,2)$， $\vec{n}=(3,5)$，则 $\vec{m}·\vec{n}=1\times 3+2\times 5=13$．

（1）已知 $\vec{m}=(2,4)$， $\vec{n}=(2,-3)$，求 $\vec{m}·\vec{n}$；

（2）已知 $\vec{m}=(x-a,1)$， $\vec{n}=(x-a,x+1)$，求 $y=\vec{m}·\vec{n}$，问 $y=\vec{m}·\vec{n}$的函数图象与一次函数 $y=x-1$的图象是否相交，请说明理由．

已知关于 $x$的一元二次方程 $x^2-6x+(2m+1)=0$有实数根．

（1）求 $m$的取值范围；

（2）如果方程的两个实数根为 $x_1$， $x_2$，且 $2x_1{x}_2+x_1+x_2⩾20$，求 $m$的取值范围．

已知关于x的方程 $x^2\mathit{﹣（}2m+1）x+m（m+1\mathit{）＝}0$．

（1）求证：方程总有两个不相等的实数根；

（2）已知方程的一个根为 $x＝0$，求代数式 $（2m﹣1{）}^2+（3+m\mathit{）（}3﹣m）+7m﹣5$的值（要求先化简再求值）．