20名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.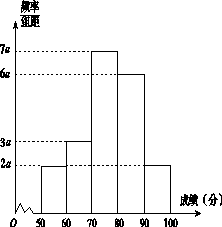
(1)求频率分布直方图中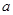 的值;
的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数.
某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
 (月) (月) |
 |
 |
 |
 |
 |
 (千克) (千克) |
 |
 |
 |
 |
 |
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图.

(2)请根据上表提供的数据,用最小二乘法求出变量 关于变量
关于变量 的线性回归直线方程
的线性回归直线方程 .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: ,
, ,
, ,
, ,
, ,
,
如图所示,椭圆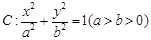 与直线
与直线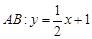 相切于点
相切于点 .
.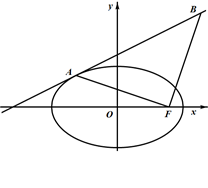
(1)求 满足的关系式,并用
满足的关系式,并用 表示点
表示点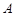 的坐标;
的坐标;
(2)设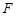 是椭圆的右焦点,若
是椭圆的右焦点,若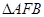 是以
是以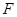 为直角顶点的等腰直角三角形,求椭圆
为直角顶点的等腰直角三角形,求椭圆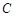 的标准方程.
的标准方程.
已知椭圆 的右焦点为
的右焦点为 ,
, 为短轴的一个端点,且
为短轴的一个端点,且 ,
, 的面积为1(其中
的面积为1(其中 为坐标原点).
为坐标原点).
(1)求椭圆的方程;
(2)若 ,
, 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 满足
满足 ,连接
,连接 ,交椭圆于点
,交椭圆于点 ,证明:
,证明: 为定值.
为定值.
已知函数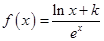 (其中
(其中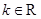 ,
, 是自然对数的底数),
是自然对数的底数),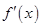 为
为 导函数.
导函数.
(1)当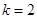 时,求曲线
时,求曲线 在点
在点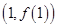 处的切线方程;
处的切线方程;
(2)若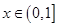 时,
时,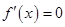 都有解,求
都有解,求 的取值范围;
的取值范围;
(3)若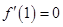 ,试证明:对任意
,试证明:对任意 ,
,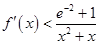 恒成立.
恒成立.
已知等差数列 的前
的前 项和为
项和为 ,并且
,并且 ,
, ,数列
,数列 满足:
满足: ,
, ,记数列
,记数列 的前
的前 项和为
项和为 .
.
(Ⅰ)求数列 的通项公式
的通项公式 及前
及前 项和公式
项和公式 ;
;
(Ⅱ)求数列 的通项公式
的通项公式 及前
及前 项和公式
项和公式 ;
;
(Ⅲ)记集合 ,若
,若 的子集个数为16,求实数
的子集个数为16,求实数 的取值范围。
的取值范围。
某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了n人,回答问题计结果如下图表所示:
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组
至少有1人获得幸运奖的概率.