如图,在透明塑料制成的长方体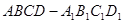 容器内灌进一些水,将容器底面一边
容器内灌进一些水,将容器底面一边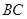 固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: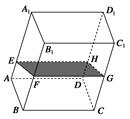
①水的部分始终呈棱柱状;
②水面四边形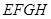 的面积不改变;
的面积不改变;
③棱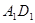 始终与水面
始终与水面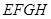 平行;
平行;
④当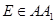 时,
时,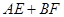 是定值.
是定值.
其中正确说法是 .
如图放置的边长为1的正方形PABC沿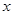 轴滚动。设顶点P(
轴滚动。设顶点P(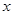 ,y)的轨迹方程是
,y)的轨迹方程是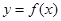 ,则
,则 的最小正周期为 ;
的最小正周期为 ;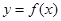 在其两个相邻零点间的图像与
在其两个相邻零点间的图像与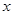 轴所围区域的面积为 。
轴所围区域的面积为 。 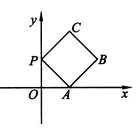
说明:“正方形PABC沿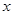 轴滚动”包括沿
轴滚动”包括沿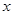 轴正方向和沿
轴正方向和沿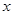 轴负方向滚动。沿
轴负方向滚动。沿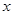 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在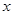 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿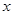 轴负方向滚动。
轴负方向滚动。
已知椭圆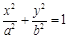
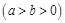 的右焦点为
的右焦点为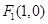 ,离心率为
,离心率为 .设A,B为椭圆上关于原点对称的两点,
.设A,B为椭圆上关于原点对称的两点,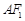 的中点为M,
的中点为M,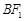 的中点为N,原点
的中点为N,原点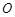 在以线段
在以线段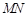 为直径的圆上.设直线AB的斜率为k,若
为直径的圆上.设直线AB的斜率为k,若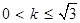 ,则
,则 的取值范围为
的取值范围为 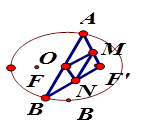
如图,在直角梯形ABCD中,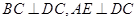 ,M、N分别是AD、AE的中点,将三角形ADE沿AE折起,下列说法正确的是 (填上所有正确的序号)。
,M、N分别是AD、AE的中点,将三角形ADE沿AE折起,下列说法正确的是 (填上所有正确的序号)。
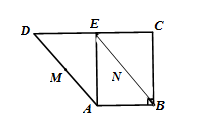
①不论D折至何位置(不在平面ABC内)都有 ;
;
②不论D折至何位置都有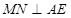 ;
;
③不论D折至何位置(不在平面ABC内)都有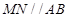 ;
;
④在折起过程中,一定存在某个位置,使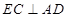 。
。
“无字证明”(proofs without words), 就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.请利用图甲、图乙中阴影部分的面积关系,写出该图所验证的一个三角恒等变换公式: .

.以下四个关于圆锥曲线的命题中:
①设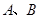 为两个定点,
为两个定点,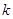 为非零常数,
为非零常数,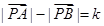 ,则动点
,则动点 的轨迹为双曲线;
的轨迹为双曲线;
②过定圆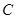 上一定点
上一定点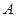 作圆的动点弦
作圆的动点弦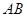 ,
, 为坐标原点,若
为坐标原点,若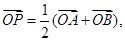 则动点
则动点 的轨迹为圆;
的轨迹为圆;
③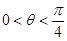 ,则双曲线
,则双曲线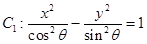 与
与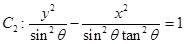 的离心率相同;
的离心率相同;
④已知两定点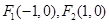 和一动点
和一动点 ,若
,若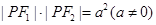 ,则点
,则点 的轨迹关于原点对称.
的轨迹关于原点对称.
其中真命题的序号为 (写出所有真命题的序号).
圆锥曲线中不同曲线的性质都是有一定联系的,比如圆可以看成特殊的椭圆,所以很多圆的性质结论可以类比到椭圆,例如;如图所示,椭圆C: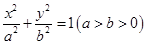 可以被认为由圆
可以被认为由圆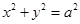 作纵向压缩变换或由圆
作纵向压缩变换或由圆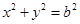 作横向拉伸变换得到的。依据上述论述我们可以推出椭圆C的面积公式为 .
作横向拉伸变换得到的。依据上述论述我们可以推出椭圆C的面积公式为 .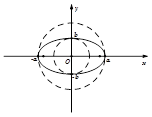
以下三个关于圆锥曲线的命题中:
①A、B为两个定点,K为非零常数,若|PA|-|PB|=K,则动点P的轨迹是双曲线。
②方程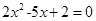 的两根可分别作为椭圆和双曲线的离心率
的两根可分别作为椭圆和双曲线的离心率
③双曲线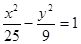 与椭圆
与椭圆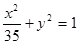 有相同的焦点。
有相同的焦点。
④已知抛物线y2=2px,以过焦点的一条弦AB为直径作圆,则此圆与准线相切
其中真命题为 (写出所有真命题的序号)