(本小题满分13分)设数列 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数 的图象上
的图象上
(1)求 归纳数列
归纳数列 的通项公式(不必证明);
的通项公式(不必证明);
(2)将数列 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为( ),
), ,
, ,
,  ;
; ,
, ,
, ,
, ;
; , ..,
, ..,
分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;
的值;
(3)设 为数列
为数列 的前
的前 项积,若不等式
项积,若不等式 对一切
对一切  都成立,其中
都成立,其中 ,求
,求 的取值范围
的取值范围
(本小题满分14分)设函数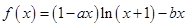 ,其中
,其中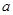 和
和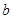 是实数,曲线
是实数,曲线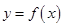 恒与
恒与 轴相切于坐标原点.
轴相切于坐标原点.
(1)求常数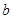 的值;
的值;
(2)当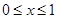 时,关于
时,关于 的不等式
的不等式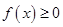 恒成立,求实数
恒成立,求实数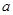 的取值范围;
的取值范围;
(3)求证: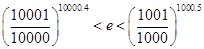 .
.
(本题满分12分)
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)设函数 ,若
,若 ,使得
,使得 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(3)若方程 有两个不相等的实数根
有两个不相等的实数根 ,求证:
,求证:
(本小题满分12分)
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取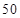 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为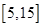 ,
,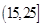 ,
, ,
,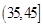 ,由此得到样本的重量频率分布直方图(如下图),
,由此得到样本的重量频率分布直方图(如下图),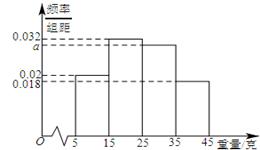
(1)求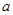 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
(2)从盒子中随机抽取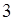 个小球,其中重量在
个小球,其中重量在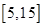 内的小球个数为
内的小球个数为 ,求
,求 的分布列和数学期望. (以直方图中的频率作为概率).
的分布列和数学期望. (以直方图中的频率作为概率).
(本小题满分16分)
对于函数 ,如果它们的图象有公共点P,且在点P处的切线相同,则称函数
,如果它们的图象有公共点P,且在点P处的切线相同,则称函数 和
和 在点P处相切,称点P为这两个函数的切点.设函数
在点P处相切,称点P为这两个函数的切点.设函数 ,
, .
.
(1)当 ,
, 时,判断函数
时,判断函数 和
和 是否相切?并说明理由;
是否相切?并说明理由;
(2)已知 ,
, ,且函数
,且函数 和
和 相切,求切点P的坐标;
相切,求切点P的坐标;
(3)设 ,点P的坐标为
,点P的坐标为 ,问是否存在符合条件的函数
,问是否存在符合条件的函数 和
和 ,使得它们在点P处相切?若点P的坐标为
,使得它们在点P处相切?若点P的坐标为 呢?(结论不要求证明)
呢?(结论不要求证明)
(本小题满分16分)
如图(1),有一块形状为等腰直角三角形的薄板,腰AC的长为a米(a为常数),现在斜边AB上选一点D,将△ACD沿CD折起,翻扣在地面上,做成一个遮阳棚,如图(2). 设△BCD的面积为S,点A到直线CD的距离为d. 实践证明,遮阳效果y与S、d的乘积Sd成正比,比例系数为k(k为常数,且k>0).
(1)设∠ACD= ,试将S表示为
,试将S表示为 的函数;
的函数;
(2)当点D在何处时,遮阳效果最佳(即y取得最大值)?
(本小题满分14分)已知数列 (
( ,
,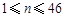 )满足
)满足 ,
,  其中
其中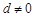 ,
, .
.
(1)当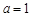 时,求
时,求 关于
关于 的表达式,并求
的表达式,并求 的取值范围;
的取值范围;
(2)设集合 .
.
①若 ,
, ,求证:
,求证: ;
;
②是否存在实数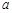 ,
, ,使
,使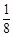 ,
,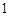 ,
,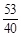 都属于
都属于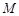 ?若存在,请求出实数
?若存在,请求出实数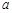 ,
, ;若不存在,请说明理由.
;若不存在,请说明理由.
如图,在 地正西方向
地正西方向 的
的 处和正东方向
处和正东方向 的
的 处各一条正北方向的公路
处各一条正北方向的公路 和
和 现计划在
现计划在 和
和 路边各修建一个物流中心
路边各修建一个物流中心 和
和 .为缓解交通压力,决定修建两条互相垂直的公路
.为缓解交通压力,决定修建两条互相垂直的公路 和
和 设
设

(1)为减少周边区域的影响,试确定 的位置,使△
的位置,使△ 与△
与△ 的面积之和最小;
的面积之和最小;
(2)为节省建设成本,试确定 的位置,使
的位置,使 的值最小.
的值最小.
已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为 和
和 ,
,
且满足 ·
· ="t" (t≠0且t≠-1).
="t" (t≠0且t≠-1).
(1)求动点P的轨迹C的方程;
(2)当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,
求t的取值范围.
(本小题满分13分)设椭圆C1: 的左、右焦点分别是F1、F2,下顶点为A,线段OA 的中点为B(O为坐标原点),如图.若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA 的中点为B(O为坐标原点),如图.若抛物线C2: 与y轴的交点为B,且经过F1,F2点.
与y轴的交点为B,且经过F1,F2点.
(1)求椭圆C1的方程;
(2)设M(0, ),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求
),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求 面积的最大值.
面积的最大值.
(本小题满分12分)已知数列 的首项
的首项 ,前
,前 项和为
项和为 ,且
,且
(1)求数列 的通项公式;
的通项公式;
(2)设函数 ,
, 是函数
是函数 的导函数,令
的导函数,令 ,求数列
,求数列 的通项公式,并研究其单调性。
的通项公式,并研究其单调性。
椭圆的两个焦点分别为 ,离心率
,离心率 。
。
(1)求椭圆方程;
(2)一条不与坐标轴平行的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,且线段
,且线段 中点的横坐标为
中点的横坐标为 ,求直线
,求直线 倾斜角的取值范围。
倾斜角的取值范围。