如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点, ,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.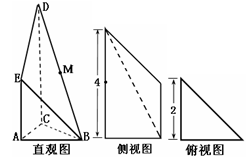
(Ⅰ)求出该几何体的体积;
(Ⅱ)试问在边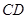 上是否存在点N,使
上是否存在点N,使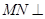 平面
平面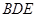 ? 若存在,确定点N的位置(不需证明);若不存在,请说明理由.
? 若存在,确定点N的位置(不需证明);若不存在,请说明理由.
如图所示,直线 与双曲线
与双曲线 及其渐近线依次交于
及其渐近线依次交于 、
、 、
、 、
、 四点,记
四点,记 .
.
(Ⅰ)若直线 的方程为
的方程为 ,求
,求 ;
;
(Ⅱ)请根据(Ⅰ)的计算结果猜想 的关系,并证明之.
的关系,并证明之.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,焦距为
轴上,焦距为 ,左顶点和上、下顶点连成的三角形为正三角形.
,左顶点和上、下顶点连成的三角形为正三角形.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若对于点 ,存在
,存在 轴上的另一点
轴上的另一点 ,使得过
,使得过 点的任意直线
点的任意直线 ,当
,当 与椭圆
与椭圆 交于相异两点
交于相异两点 、
、 时,
时, 为定值,求
为定值,求 的取值范围.
的取值范围.
在平面直角坐标系xoy中,点P到两点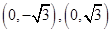 的距离之和等于4,设点P的轨迹为C.
的距离之和等于4,设点P的轨迹为C.
(1)写出C的方程;
(2)设直线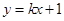 与C交于A,B两点,k为何值时以线段AB为直径的圆过原点?
与C交于A,B两点,k为何值时以线段AB为直径的圆过原点?
求下列曲线的标准方程:
(1)两个焦点的坐标分别是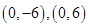 ,且双曲线过点
,且双曲线过点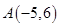 ,求双曲线的标准方程;
,求双曲线的标准方程;
(2)求以原点为顶点,以坐标轴为对称轴,且焦点在直线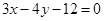 上的抛物线的标准方程.
上的抛物线的标准方程.
在平面直角坐标系xoy中,点A,B的坐标分别是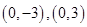 ,直线AM、BM相交于点M,且它们的斜率之积是
,直线AM、BM相交于点M,且它们的斜率之积是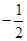 .
.
(1)求 M的轨迹C方程;
(2)若直线l经过点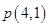 ,与轨迹C有且仅有一个公共点,求直线l的方程.
,与轨迹C有且仅有一个公共点,求直线l的方程.
已知F1、F2是椭圆 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足 (O是坐标原点),
(O是坐标原点), 若椭圆的离心率等于
若椭圆的离心率等于
(1)求直线AB的方程;
(2)若三角形ABF2的面积等于 ,求椭圆的方程.
,求椭圆的方程.
已知椭圆 的中心在坐标原点
的中心在坐标原点 ,焦点在坐标轴上,且经过
,焦点在坐标轴上,且经过 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)已知定点 ,
, 点为椭圆上的动点,求
点为椭圆上的动点,求 最大值及相应的
最大值及相应的 点坐标.
点坐标.
已知函数 (
( 为常数),其图象是曲线
为常数),其图象是曲线 .
.
(1)当 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(2)设函数 的导函数为
的导函数为 ,若存在唯一的实数
,若存在唯一的实数 ,使得
,使得 与
与 同时成立,求实数
同时成立,求实数 的取值范围;
的取值范围;
(3)已知点 为曲线
为曲线 上的动点,在点
上的动点,在点 处作曲线
处作曲线 的切线
的切线 与曲线
与曲线 交于另一点
交于另一点 ,在点
,在点 处作曲线
处作曲线 的切线
的切线 ,设切线
,设切线 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知函数 ,(
,( 为常数).
为常数).
(1)若 在
在 处的切线过点(0,-5),求
处的切线过点(0,-5),求 的值;
的值;
(2)设函数 的导函数为
的导函数为 ,若关于
,若关于 的方程
的方程 有唯一解,求实数
有唯一解,求实数 的取值范围;
的取值范围;
(3)令 ,若函数
,若函数 存在极值,且所有极值之和大于
存在极值,且所有极值之和大于 ,求实数
,求实数 的取值范围.
的取值范围.