已知椭圆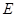
的中心在原点，焦点在
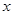轴上，焦距为
，左顶点和上、下顶点连成的三角形为正三角形．
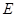（Ⅰ）求椭圆的方程；
（Ⅱ）若对于点
，存在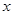轴上的另一点
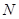，使得过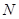点的任意直线
，当与椭圆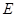交于相异两点
、
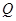时，
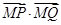为定值，求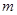
的取值范围．
相关试题
中，
，
，且公比
．
，求
的最大值及相应的
值．
中，
，
，
是
的中点，
在线段
上且
．
面
；
的大小．
、
、
分别是角
、
、
所对的边．已知
．
，△ABC的面积为
，求
的值．
．
的奇偶性；
上增减性，并进行证明；
时，不等式
恒成立，求实数
的取值范围．
，已知到今年为止，森林剩余面积为原来的
．推荐套卷
已知椭圆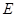的中心在原点，焦点在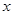轴上，焦距为，左顶点和上、下顶点连成的三角形为正三角形．
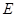（Ⅰ）求椭圆的方程；
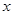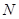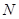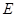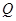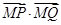（Ⅱ）若对于点，存在轴上的另一点，使得过点的任意直线，当与椭圆交于相异两点、时，为定值，求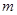的取值范围．
粤公网安备 44130202000953号