
(本小题满分12分)
如图所示,已知圆 :
: ,直线
,直线 :
: 是圆的一条切线,且
是圆的一条切线,且 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,
, .
.
(1)若弦 的长为
的长为 ,求直线
,求直线 的方程;
的方程;
(2)当直线 满足条件(1)时,求
满足条件(1)时,求 的值.
的值.
椭圆的中心在原点,焦点F在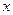 轴上,离心率为
轴上,离心率为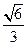 ,点
,点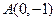 到F点的距离为
到F点的距离为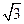 ,(1)求椭圆的方程;
,(1)求椭圆的方程;
(2)直线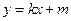 与椭圆交于不同的两点M、N两点,若
与椭圆交于不同的两点M、N两点,若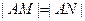 ,求实数
,求实数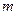 的取值范围。
的取值范围。
抛物线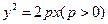 的焦点与椭圆
的焦点与椭圆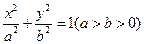 的一个焦点重合,且抛物线与椭圆的一个交点为
的一个焦点重合,且抛物线与椭圆的一个交点为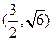 ,(1)求抛物线与椭圆的方程,(2)若过点
,(1)求抛物线与椭圆的方程,(2)若过点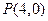 的直线与抛物线交于点
的直线与抛物线交于点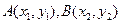 ,求
,求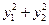 的最小值
的最小值
已知实数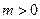 ,命题
,命题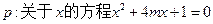 有两个不同的的实数根;
有两个不同的的实数根;
命题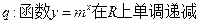 。若
。若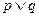 为真,
为真,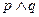 为假,求
为假,求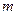 的取值范围。
的取值范围。
(本小题满分12分)
如图,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是直线 上任意一点,过点M引抛物线E的两条切线分别交x轴于点S , T,切点分别为B、A。
上任意一点,过点M引抛物线E的两条切线分别交x轴于点S , T,切点分别为B、A。
(1)求抛物线E的方程;
(2)求证:点S,T在以FM为直径的圆上;
(3)当点M在直线 上移动时,直线AB恒过焦点F,求
上移动时,直线AB恒过焦点F,求 的值。
的值。
(本小题满分12 分)
分)
设函数f(x)的定义域为R,若|f(x)|≤|x|对任意的实数x均成立,则称函数f(x)为 函数。
函数。
(1)试判断函数 =
=
 =
= 中哪些是
中哪些是 函数,并说明理由;
函数,并说明理由;
(2)求证:若a>1,则函数f(x)=ln(x2+a)-lna是 函数。
函数。
(本小题满分12分)
将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结EB、FB、FA后围成一个空间几何体如图2所示,
(1)求异面直线BD与EF所成角的大小;
(2)求二面角D—BF—E的大小;
(3)求这个几何体的体积.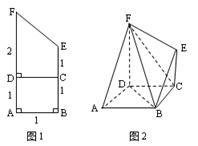
(本小题满分12分)
从集合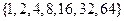 的所有非空真子集中等可能地取出一个.
的所有非空真子集中等可能地取出一个.
(1)求所取的子集中元素从小到大排列成等 比数列的概率;
比数列的概率;
(2)记所取出的子集的元素个数为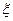 ,求
,求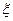 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
在锐角△ABC 中,已知内角
中,已知内角 A、B、C的对边分别为a、b、c.向量
A、B、C的对边分别为a、b、c.向量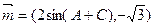 ,
,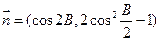 ,且向量
,且向量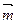 、
、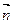 共线。
共线。
(1)求角B的大小;
(2)如果b=1,求△ABC的面积S△ABC的最大值。
(本小题共13分)
设集合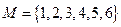 ,对于
,对于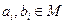 ,记
,记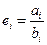 且
且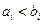 ,由所有
,由所有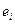 组成的集合设为
组成的集合设为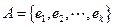 .
.
(Ⅰ)求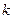 的值;
的值;
(Ⅱ)设集合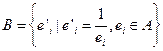 ,对任意
,对任意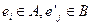 ,试求
,试求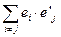 ;
;
(Ⅲ)设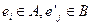 ,试求
,试求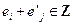 的概率.
的概率.
(本小题共14分)
已知椭圆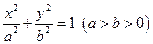 和圆
和圆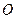 :
: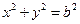 ,过椭圆上一点
,过椭圆上一点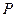 引圆
引圆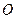 的两条切线,切点分别为
的两条切线,切点分别为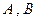 .
.
(Ⅰ)(ⅰ)若圆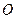 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率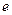
 ;
;
(ⅱ)若椭圆上存在点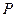 ,使得
,使得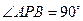 ,求椭圆离心率
,求椭圆离心率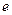 的取值范围;
的取值范围;
(Ⅱ)设直线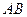 与
与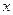 轴、
轴、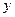 轴分别交于点
轴分别交于点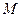 ,
,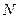 ,求证:
,求证: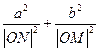 为定值.
为定值.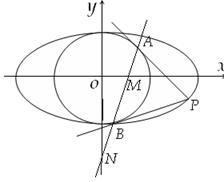
( 本小题共13分)
本小题共13分)
某学校高一年级开设了 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修
五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修 一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
(Ⅰ)求甲、乙、丙三名学生参加五门选修课的所有选法种数;
(Ⅱ)求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率;
(Ⅲ)设随机变量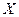 为甲、乙、丙这三名学生参加
为甲、乙、丙这三名学生参加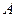 课程的人数,求
课程的人数,求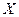 的分布列与数学期望.
的分布列与数学期望.