(本小题满分13分 )对于给定数列
)对于给定数列 ,如果存在实常数
,如果存在实常数 使得
使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “M类数列”.
是 “M类数列”.
(1)若 ,
, (
( ),数列
),数列 、
、 是否为“M类数列”?若是,指出它对应的实
是否为“M类数列”?若是,指出它对应的实 常数
常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列 是“M类数
是“M类数 列”,则数列
列”,则数列 也是“M类数列”;
也是“M类数列”;
(3)若数列 满足
满足 ,
,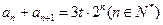 ,
, 为常数,求数列
为常数,求数列 前
前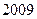 项的和,并判断
项的和,并判断 是否为“M类数列”,说明理由.
是否为“M类数列”,说明理由.
(本小题满分13分)设椭圆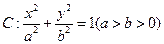 的上顶点为
的上顶点为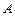 ,椭圆
,椭圆 上两点
上两点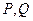 在
在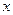 轴上的射影分别为左焦点
轴上的射影分别为左焦点 和右焦点
和右焦点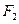 ,直线
,直线 的斜率为
的斜率为 ,过点
,过点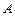 且与
且与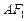 垂直的直线与
垂直的直线与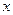 轴交于点
轴交于点 ,
, 的外接圆为圆
的外接圆为圆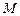 .
.
(1)求椭圆的离心率;
(2)直线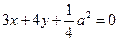 与圆
与圆 相交于
相交于 两点,且
两点,且 ,求椭圆方程;
,求椭圆方程;
(3)设点 在椭圆C内部,若椭圆C上的点到点N的最远距离不大于
在椭圆C内部,若椭圆C上的点到点N的最远距离不大于 ,求椭圆C的短轴长的取值范围.
,求椭圆C的短轴长的取值范围.
(本小题满分13分)已知函数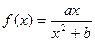 在
在 处取得极值2.
处取得极值2.
(1)求函数 的表达式;
的表达式;
(2)当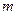 满足什么条件时,函数
满足什么条件时,函数 在区间
在区间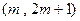 上单调递增?
上单调递增?
(3)若 为
为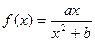 图象上任意一点,直线
图象上任意一点,直线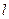 与
与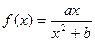 的图象切于点
的图象切于点 ,求直线
,求直线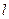 的斜率
的斜率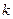 的取值范围.
的取值范围.
(本小题满分12分)如图,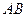 为圆
为圆 的直径,点
的直径,点 、
、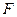 在圆
在圆 上,
上, ,矩形
,矩形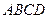 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
, .
.
(1) 求证:
求证: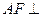 平面
平面 ;
;
(2)设 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;
(3)设平面 将几何体
将几何体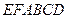 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为 ,
, ,求
,求
 .
.
(本小题满分12分)某学校高一、高二、高三的三个年级学生人数如下表
| |
高三 |
高二 |
高一 |
| 女生 |
100 |
150 |
z |
| 男生 |
300 |
450 |
600 |
按年级分层抽样的方法评选优秀学生50人,其中高三有10人.
(1)求z的值;
(2)用分层抽样的方法在高一中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1名女生的概率;
(3)用随机抽样的方法从高二女生中抽取8人,经检测她们的得分如下:9.4,8.6,9.2, 9.6,8.7,9.3 ,9.0,8.2,把这8人的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
,9.0,8.2,把这8人的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
(本小题满分12分)已知在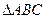 中,
中, ,
,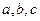 分别是角
分别是角 所对的边.
所对的边.
(1)求 ;
;
(2)若 ,
, ,求
,求 的面积
的面积 .
.
(本小题满分12分)
已知数列 满足:
满足: ,且对一切
,且对一切 ,有
,有 ,其中
,其中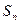 为数列
为数列 的前
的前 项和.(Ⅰ)求数列
项和.(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)证明: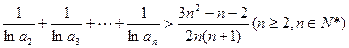 .
.
(本小题满分12分)
已知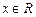 ,函数
,函数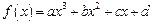 在
在 处取得极值,曲线
处取得极值,曲线 过原点
过原点 和点
和点 .若曲线
.若曲线 在点
在点 处的切线
处的切线 与直线
与直线 的夹角为
的夹角为 ,且直线
,且直线 的倾斜角
的倾斜角 (Ⅰ)求
(Ⅰ)求 的解析式;(Ⅱ)若函数
的解析式;(Ⅱ)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围;(Ⅲ)若
的取值范围;(Ⅲ)若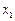 、
、 ,求证:
,求证:
(本小题满分13分) 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.
SD=2,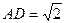 ,E是SD上的点.(Ⅰ)求证:AC⊥BE;
,E是SD上的点.(Ⅰ)求证:AC⊥BE;
(Ⅱ)求二面角C—AS—D的余弦值.
某人为了获得国外某大学的留学资格,必须依次通过科目一、科目二、科目三3次考试,若某科目考试没通过,则不能参加后面科目的考试,已知他通过科目一、科目二、科目三考试的概率分别为0.9、0.7、0.6.(Ⅰ)求此人顺利获得留学资格的概率;(Ⅱ)设此人在此次申请留学资格的过程中,参加的考试次数为随机变量 ,求
,求 的数学期望.
的数学期望.
已知a、b、c是△ABC三边长,关于x的方程
 的两根之差的平方等于4,△ABC的面积
的两根之差的平方等于4,△ABC的面积 (I)求
(I)求 C;(II)求a、b的值.
C;(II)求a、b的值.
22.(本小题满分12分)
A、B是双曲线 ―y2=1上两点,M为该双曲线右准线上一点,且
―y2=1上两点,M为该双曲线右准线上一点,且 =
= .
.
(Ⅰ)求| |的取值范围(O为坐标原点);
|的取值范围(O为坐标原点);
(Ⅱ)是否存在定点N,使|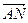 |=|
|=| |总成立?并说明理由.
|总成立?并说明理由.
21.(本小题满分12分)
已知函数f(x)= 在x=1处取得极值(a>0)
在x=1处取得极值(a>0)
(I)求a、b所满足的条件;
(II)讨论函数f(x)的单调性.
20.(本小题满分12分)
已知数列{an}的前n项和Sn=3―an― ,
,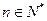 .
.
(I)求证: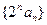 是等差数列;
是等差数列;
(II)求an的最大值.