重庆市高考数学理科考试试题(样卷)
容量为 的样本数据,依次分为
的样本数据,依次分为 组,如下表:
组,如下表:
| 组号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 频数 |
10 |
13 |
 |
 |
15 |
13 |
12 |
9 |
则第三组的频率是( ▲ )
| A.0.28 | B.0.12 | C.0.15 | D.0.21 |
将正方形ABCD沿对角线AC折成一个直二面角,则异面直线AB和CD所成的角是( ▲ )
A. |
B. |
C. |
D. |
已知函数 是周期为4的函数,
是周期为4的函数,
其部分图象如右图,给出下列命题:①是奇函数;
② 的值域是
的值域是 ;③关于
;③关于 的方程
的方程 必有实根;
必有实根;
④关于 的不等式
的不等式 的解集非空。其中正确命题的个数为( ▲ )
的解集非空。其中正确命题的个数为( ▲ )
| A.4 | B.3 | C.2 | D.1 |
双曲线具有光学性质:“从双曲线的一个焦点发出的光线经过双曲线反射后,反射光线的反向延长线都汇聚到双曲线的另一个焦点。”由此可得如下结论:如右图,过双曲线 :
: 右支上的点
右支上的点 的切线
的切线 平分
平分 。现过原点作
。现过原点作 的平行线交
的平行线交 于
于 ,则
,则 等于( ▲ )
等于( ▲ )
A. |
B. |
C. |
D.与点 的位置有关 的位置有关 |
在0, 1,2,3,4,5这六个数字所组成的没有重复数字的三位数中,其各个数字之和为9的三位数共有 ▲ 个(用数字做答)
已知a、b、c是△ABC三边长,关于x的方程
 的两根之差的平方等于4,△ABC的面积
的两根之差的平方等于4,△ABC的面积 (I)求
(I)求 C;(II)求a、b的值.
C;(II)求a、b的值.
某人为了获得国外某大学的留学资格,必须依次通过科目一、科目二、科目三3次考试,若某科目考试没通过,则不能参加后面科目的考试,已知他通过科目一、科目二、科目三考试的概率分别为0.9、0.7、0.6.(Ⅰ)求此人顺利获得留学资格的概率;(Ⅱ)设此人在此次申请留学资格的过程中,参加的考试次数为随机变量 ,求
,求 的数学期望.
的数学期望.
(本小题满分13分) 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.
SD=2,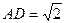 ,E是SD上的点.(Ⅰ)求证:AC⊥BE;
,E是SD上的点.(Ⅰ)求证:AC⊥BE;
(Ⅱ)求二面角C—AS—D的余弦值.
(本小题满分12分)
已知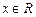 ,函数
,函数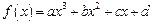 在
在 处取得极值,曲线
处取得极值,曲线 过原点
过原点 和点
和点 .若曲线
.若曲线 在点
在点 处的切线
处的切线 与直线
与直线 的夹角为
的夹角为 ,且直线
,且直线 的倾斜角
的倾斜角 (Ⅰ)求
(Ⅰ)求 的解析式;(Ⅱ)若函数
的解析式;(Ⅱ)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围;(Ⅲ)若
的取值范围;(Ⅲ)若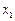 、
、 ,求证:
,求证:
(本小题满分12分)已知椭圆 经过点
经过点 ,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
(1)求椭圆的方程;
(2)动直线 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
 的定义域为A,函数
的定义域为A,函数 的定义域为B,则A
的定义域为B,则A B=( ▲ )
B=( ▲ )



 的反函数是( ▲ )
的反函数是( ▲ )



 中,
中, ,则
,则 等于( ▲ )
等于( ▲ ) 表示虚数单位),那么
表示虚数单位),那么 ( ▲ )
( ▲ )

 ,则函数
,则函数 的值域为( ▲ )
的值域为( ▲ )



 是直线
是直线 上的动点,
上的动点, 是圆
是圆 的两条切线(
的两条切线( 为切点),则四边形
为切点),则四边形 面积的最小值( ▲ )
面积的最小值( ▲ )



 的展开式中,常数项为252,则
的展开式中,常数项为252,则 ___▲___.
___▲___. 为不等式组
为不等式组 表示的平面区域,则当
表示的平面区域,则当 从-2连续变化到1时,动直线
从-2连续变化到1时,动直线 扫过
扫过 是个一元三次函数,且满足
是个一元三次函数,且满足 ,
, 在
在 上处处连续,则实数
上处处连续,则实数 的值为 ▲ .
的值为 ▲ . 中,
中, ,一条直线
,一条直线 与边
与边 分别交与点
分别交与点 ,且分
,且分 的面积为相等的两部分,则线段
的面积为相等的两部分,则线段 长的最小值为 ▲ .
长的最小值为 ▲ .
 满足:
满足: ,且对一切
,且对一切 ,有
,有 ,其中
,其中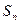 为数列
为数列 项和.(Ⅰ)求数列
项和.(Ⅰ)求数列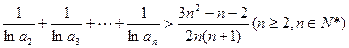 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号