2010年东北三省四市长春、哈尔滨、沈阳、大连第二次联合考试
已知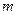 ,
,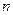 为不同直线,
为不同直线,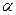 ,
,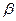 为不同平面,则下列选项:①
为不同平面,则下列选项:①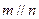 ,
, ;②
;② ,
,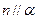 ;③
;③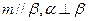 ;④
;④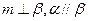 ,其中能使
,其中能使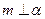 成立的充分条件有
成立的充分条件有
| A.①② | B.①③ | C.①④ | D.③④ |
函数 的零点所在的区间是
的零点所在的区间是
| A.(0,1) | B.(1,10) | C.(10,100) | D.(100, ) ) |
已知双曲线 的两个焦点分别为
的两个焦点分别为 ,
, ,
, 为双曲线上的一点,且
为双曲线上的一点,且 90°,则
90°,则
A. |
B.1 |
| C.2 | D.4 |
在 中,
中, 分别是角
分别是角 的对边,且
的对边,且  ,则
,则 一定是
一定是
| A.等边三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.无法确定 |
一组数据共有7个数,记得其中有10,2,5,2,4,2,还有一个数没记清,但知道这组数的平均数、中位数、众数依次成等差数列,这个数的所有可能值的和为
| A.9 | B.3 | C.17 | D. 11 11 |
已知定义域为 的函数
的函数 ,则下列命题正确的是:
,则下列命题正确的是:
A.若 恒成立,则函数 恒成立,则函数 的图像关于(1,0)点对称; 的图像关于(1,0)点对称; |
B.若 恒成立,则函数 恒成立,则函数 的图像关于直线 的图像关于直线 对称; 对称; |
C.函数 的图像与函数 的图像与函数 的图像关于原点对称; 的图像关于原点对称; |
D.函数 的图像与函数 的图像与函数 的图像关于 的图像关于 轴对称; 轴对称; |

如图所示,某几何体的正视图、侧视图均为半圆和等边三角形的
组合,俯视图为圆形,则该几何体的全面积为  .
.
(本小题满分12分)
已知等差数列 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设等比数列 各项均为正数,其前
各项均为正数,其前 项和
项和 ,若
,若 ,求
,求 .
.
(本小题满分12分)
网站就观众对某小品类节目的喜爱程度进行网上调查,其中持各种态度的人数如下表:
| |
喜欢 |
一般 |
不喜欢 |
| 人数 |
560 |
240 |
200 |
(1)现用分层抽样的方法从所有参与网上调查的观众中抽取了一个容量为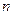 的样本,已知从不喜欢小品的观众中国抽取的人数为5人,则
的样本,已知从不喜欢小品的观众中国抽取的人数为5人,则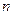 的值为多少?
的值为多少?
(2)在(1)的条件下,若抽取到的5名不喜欢小品的观众中有2名女性,现将抽取到的5名不喜欢小品的观众看成一个总体,从中任取两名观众,求至少有一名为女性观众的概率.

(本小题满分12分)
如图,在正方体 中,
中, 、
、 分别是
分别是 、
、 中点
中点
(1)求证: ;
;
(2)求证: ;
;
(3)棱 上是否存在点
上是否存在点 ,使
,使 平面
平面 ,若存在,确 定点
,若存在,确 定点 位置;若不存在,说明理由.
位置;若不存在,说明理由.

(本小题满分12分)
如图所示,已知圆 :
: ,直线
,直线 :
: 是圆的一条切线,且
是圆的一条切线,且 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,
, .
.
(1)若弦 的长为
的长为 ,求直线
,求直线 的方程;
的方程;
(2)当直线 满足条件(1)时,求
满足条件(1)时,求 的值.
的值.
本小题满分12分)
已知函数 ,其中
,其中 为常数,
为常数, 为自然对数的底数.
为自然对数的底数.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 在区间
在区间 上的最大值为2,求
上的最大值为2,求 的值.
的值.

(本小题满分10分)选修4—1:几何证明选讲
如图,梯形 内接于
内接于 ,
, ,过点
,过点 作
作 的切线,交
的切线,交 的延长线于点
的延长线于点 ,交
,交 的延长线于点
的延长线于点 .
.
(1)求证: ;
;
(2)若 ,
, ,
, ,求切线
,求切线 的长.
的长.
(本小题满分10分)选修4—4:坐标系与参数方程
已知在平面直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为 ,(
,( 为参数),以
为参数),以 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.
(1)写出直线 的直角坐标方程和圆
的直角坐标方程和圆 的普通方程;
的普通方程;
(2)求圆 截直线
截直线 所得的弦长.
所得的弦长.
 ,若
,若 为纯虚数,则实数
为纯虚数,则实数
 B
B C.
C. D.
D.
 ,且
,且 ,则
,则




 ,
, ,若
,若 ,则实数
,则实数






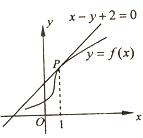
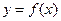 的图像在点
的图像在点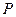 处的切线方程为
处的切线方程为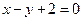 ,则
,则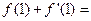
 ,
, ,设
,设 ,则下列说法不正确的是
,则下列说法不正确的是



 的最小值为 .
的最小值为 . ,若
,若 则
则
 内任投一点
内任投一点 ,则点
,则点 内的概率为 .
内的概率为 .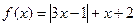 ,
,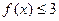 ,
,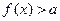 的解集为
的解集为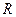 ,求
,求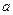 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号