设数列{an}(n∈N)满足a0=0,a1=2,且对一切n∈N,有an+2=2an+1-an+2.
(1)求数列{an}的通项公式;
(2)i当 时,令
时,令 ,
, 是数列{bn}的前n项和,求证:
是数列{bn}的前n项和,求证:
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.
(I) 求证:MN⊥平面ABCD
(II) 求线段AB的长;
(III)求二面角A-DE-B的平面角的正弦值.
已知: ,(
,( 为常数).
为常数).
(1)求 的最小正周期;
的最小正周期;
(2) 在
在 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求 的值;
的值;
(3)求在(2)条件下 的单调减区间.
的单调减区间.
某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题。
(1)求全班人数及分数在 之间的频数;
之间的频数;
(2)估计该班的平均分数,并计算频率分布的直方图中 的矩形的高;
的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率。
如图,已知四棱锥P—ABCD中,底面ABCD是直角梯长,AB//CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1。
(1)求证:BC⊥平面PAC;
(2)若M是PC的中点,求三棱锥M—ACD的体积。
已知向量m=(cosx,sinx),n=(cosx,cosx)(x∈R),设函数f(x)=m·n
(1)求 f(x)的解析式,并求最小正周期.
(2)若函数 g(x)的图像是由函数 f(x)的图像向右平移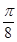 个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
在极坐标系中,过曲线L: (
( >0)外的一点A(2
>0)外的一点A(2 ,
,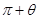 )(其中tanθ=2,θ为锐角)作平行于θ=
)(其中tanθ=2,θ为锐角)作平行于θ= (
( )的直线
)的直线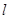 与曲线L分别交于B、C。
与曲线L分别交于B、C。
(1)写出曲线L和直线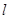 的普通方程(以极点为原点,极轴为x轴的正半轴建系);(2)若︱AB︱、︱BC︱、︱AC︱成等比数列,求
的普通方程(以极点为原点,极轴为x轴的正半轴建系);(2)若︱AB︱、︱BC︱、︱AC︱成等比数列,求 的值。
的值。