高中数学解答题

泉州市组织群众性登清源山健身活动,招募了名师生志愿者,现将所有志愿者按年龄情况分为等六组,其频率分布直方图如下图所示: 已知之间的志愿者共人.
（1）求和之间的志愿者人数;
（2）已知和之间各有名数学教师，现从这两个组中各选取人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有名数学教师的概率?
（3）组织者从之间的志愿者(其中共有名女教师，其余全为男教师)中随机选取名担任后勤保障工作,其中女教师的人数为,求的分布列和数学期望.

解关于x的不等式   

在四棱锥P－ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底 面ABCD是直角梯形，AB∥CD，∠ADC＝90°，AB＝AD＝PD＝1，CD＝2．
　　(Ⅰ)求证：BE∥平面PAD；
　　(Ⅱ)求证：BC⊥平面PBD；
　　(Ⅲ)求四棱锥P－ABCD的体积。
　

一个长、宽、高分别为a、b、c长方体的体积是8cm²，它的全面积是32 cm²， 且满足  b²＝ac，求这个长方体所有棱长之和。

已知，满足约束条件求的最小值与最大值。

在中，已知，.
(1)求的值； (2)若为的中点，求的长.

某市近郊有一块大约500m×500m的接近正方形的荒地，地方政府准备在此建一个综合性休闲广场，首先要建设如图所示的一个矩形场地，其中总面积为3000平方米，其中阴影部分为通道，通道宽度为2米，中间的三个矩形区域将铺设塑胶地面作为运动场地（其中两个小场地形状相同），塑胶运动场地占地面积为S平方米。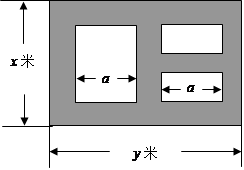

（1）分别用x表示y和S的函数关系式，并给出定义域；
（2）怎样设计能使S取得最大值，并求出最大值。

已知二次函数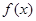的二次项系数为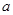，且不等式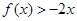的解集为．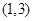
(1)若方程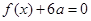有两个相等的实数根, 求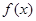的解析式；
(2)若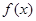的最大值为正数，求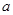的取值范围．

已知命题p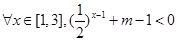：，命题q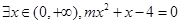：. 若“p且q”为真命题，求实数m的取值范围.

已知直线L的参数方程｛，（t为参数）圆C的极坐标方程是

试判断直线L与圆C的位置关系.

如图用n种不同颜色，给图中A、B、C、D、四块区域涂色，允许同一种颜色
涂不同区域，但相邻区域不能涂同一种颜色⑴n=3，共有多少种不同的涂法？
⑵n=5，共有多少种不同的涂法？

设复数满足，求复数及。

设函数。
（Ⅰ）求的极大值点与极小值点；
（Ⅱ）求在区间上的最大值与最小值。

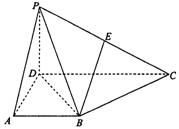
在平面内，如果用一条直线去截正方形的一个角，那么截下的一个直角三角形按图所标边长，由勾股定理有。设想正方形换成正方体，把截线换成如图所示的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥，如果用，，表示三个侧面面积，表示截面面积，那么你类比得到的结论是               。

设，集合，.
（Ⅰ）当a=3时，求集合；
（Ⅱ）若，求实数的取值范围.