在复平面内,复数 对应的点位于( )
| A. |
第一象限 |
B. |
第二象限 |
C. |
第三象限 |
D. |
第四象限 |
执行下面的程序框图,为使输出 S的值小于91,则输入的正整数 N的最小值为( )
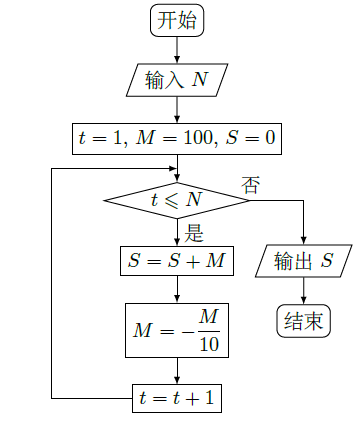
| A. | 5 |
B. | 4 |
C. | 3 |
D. | 2 |
设函数 ,则下列结论错误的是( )
| A. |
的一个周期为 |
B. |
的图像关于直线 对称 |
| C. |
的一个零点为 |
D. |
在 单调递减 |
已知双曲线 的一条渐近线方程为 ,且与椭圆 有公共焦点.则 C的方程为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
( 的展开式中 的系数为( )
| A. |
-80 |
B. |
-40 |
C. |
40 |
D. |
80 |
某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
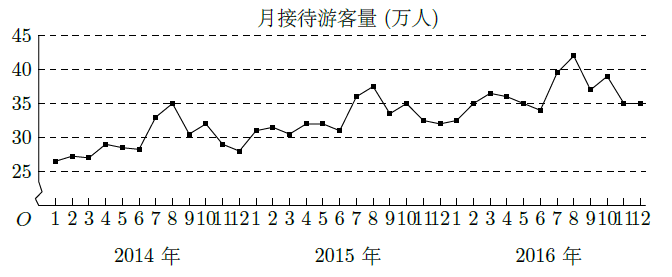
| A. | 月接待游客量逐月增加 |
| B. | 年接待游客量逐年增加 |
| C. | 各年的月接待游客量高峰期大致在7,8月 |
| D. | 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 |
已知集合 , ,则 中元素的个数为( )
| A. |
3 |
B. |
2 |
C. |
1 |
D. |
0 |
设向量 均为单位向量,则" "是" "的( )
| A. |
充分不必要条件 |
B. |
必要不充分条件 |
C. |
充要条件 |
D. |
既不充分又不必要条件 |
"十二平均律" 是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于 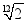 .若第一个单音的频率为 f ,则第八个单音的频率为( )
.若第一个单音的频率为 f ,则第八个单音的频率为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
在复平面内,复数 的共轭复数对应的点位于( )
| A. |
第一象限 |
B. |
第二象限 |
| C. |
第三象限 |
D. |
第四象限 |
已知集合 , ,则 ( )
| A. | {0,1} |
B. | {−1,0,1} |
| C. | {−2,0,1,2} |
D. | {−1,0,1,2} |