已知数列 的前
的前 项和为
项和为 ,点
,点 在直线
在直线 上.数列
上.数列 满足
满足
 ,
, ,且其前9项和为153.
,且其前9项和为153.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,求使不等式
,求使不等式 对一切
对一切 都成立的最大正整数
都成立的最大正整数 的值.
的值.
两台机床同时生产直径为10的零件,为了检验产品质量,质量质检员从两台机床的产品中各抽取4件进行测量,结果如下:
| 机床甲 |
10 |
9.8 |
10 |
10.2 |
| 机床乙 |
10.1 |
10 |
9.9 |
10 |
如果你是质量检测员,在收集到上述数据后,你将通过怎样的运算来判断哪台机床生产的零件质量更符合要求.
(本小题满分14分)
已知函数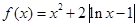 .
.
(1)求函数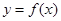 的最小值;
的最小值;
(2)证明:对任意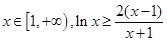 恒成立;
恒成立;
(3)对于函数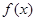 图象上的不同两点
图象上的不同两点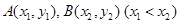 ,如果在函数
,如果在函数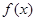 图象上存在点
图象上存在点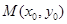 (其中
(其中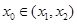 )使得点
)使得点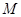 处的切线
处的切线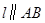 ,则称直线
,则称直线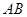 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当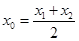 时,又称直线
时,又称直线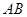 存在“中值伴侣切线”.试问:当
存在“中值伴侣切线”.试问:当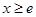 时,对于函数
时,对于函数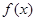 图象上不同两点
图象上不同两点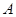 、
、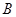 ,直线
,直线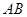 是否存在“中值伴侣切线”?证明你的结论.
是否存在“中值伴侣切线”?证明你的结论.
(本小题满分12分)
已知函数 .
.
(1)若函数 的图象在
的图象在 处的切线斜率为
处的切线斜率为 ,求实数
,求实数 的值;
的值;
(2)在(1)的条件下,求函数 的单调区间;
的单调区间;
(3)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围.
的取值范围.
(本小题满分12分)
如图,在四棱锥S—ABCD中, 底面ABCD,底面ABCD是矩形,
底面ABCD,底面ABCD是矩形, ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED 平面SAB;
平面SAB;
(2)求直线SA与平面BED所成角的大小.