已知各项不为零的数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,数列
,数列 满足
满足 ,数列
,数列 的前
的前 项和
项和
(Ⅰ)求
(Ⅱ)若 ,不等式
,不等式 恒成立,求使关于
恒成立,求使关于 的不等式有解的充要条件.
的不等式有解的充要条件.
(本小题满分12分)
平面直角坐标系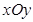 中,过椭圆
中,过椭圆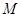 :
: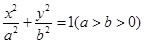 右焦点的直线
右焦点的直线 交
交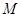 于
于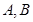 两点,
两点, 为
为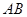 的中点,且
的中点,且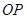 的斜率为
的斜率为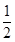 .
.
(Ⅰ)求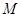 的方程;
的方程;
(Ⅱ)若 ,
, 为
为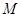 上的两点,若四边形
上的两点,若四边形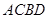 的对角线
的对角线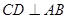 ,求四边形
,求四边形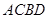 面积的最大值.
面积的最大值.
若某产品的直径长与标准值的差的绝对值不超过 时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:
时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位: )将所得数据分组,得到如下频率分布表:
)将所得数据分组,得到如下频率分布表:
(1)将上面表格中缺少的数据填充完整;
(2)估计该厂生产的此种产品中,不合格的直径长与标准值的差落在区间 内的概率
内的概率
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品,据此估算这批产品中的合格品的件数.
已知过点 的直线
的直线 交抛物线
交抛物线 于
于 两点,直线
两点,直线 交
交 轴于点
轴于点 .
.
(1)设直线 的斜率分别为
的斜率分别为 ,求
,求 的值;
的值;
(2)点 为抛物线
为抛物线 上异于
上异于 的任意一点,直线
的任意一点,直线 交直线
交直线 于
于 两点,
两点, ,求抛物线
,求抛物线 的方程.
的方程.
已知函数f(x)= 和函数g(x)=x|x﹣m|+2m﹣8,其中m为参数,且满足m≤5.
和函数g(x)=x|x﹣m|+2m﹣8,其中m为参数,且满足m≤5.
(1)若m=2,写出函数g(x)的单调区间(无需证明);
(2)若方程f(x)= 在x∈[﹣2,+∞)上有唯一解,求实数m的取值范围;
在x∈[﹣2,+∞)上有唯一解,求实数m的取值范围;
(3)若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得f(x2)=g(x1)成立,求实数m的取值范围.
设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若 是
是 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.