高中数学解答题

计算：
（1）；
（2）．

已知f（x）是二次函数，不等式f（x）＜0的解集是（0,5），且f（x）在区间[－1,4]上的最大值是12．
（Ⅰ）求f（x）的解析式；
（Ⅱ）求f（x）在区间上的最小值．

邵东某桶装水经营部每天的房租、人员工资等固定成本为360元，每桶水进价4元，销售单价与日均销量的关系如表所示

销售单价/元	5	6	7	8	9	10	11
日均销售量/桶	360	320	280	240	200	160	120

 
请根据以上数据作出分析，这个经营部怎样定价（单价要为整元）才能获得最大利润？最大利润为多少？

如图，在四棱锥中，底面是正方形，侧面底面，且，、分别为、的中点．

（Ⅰ）求证：直线∥平面；
（Ⅱ）求证：直线平面．

已知以点C为圆心的圆经过点A（3，1）和B（1，3），且圆自身关于直线对称．设直线：．
（1）求圆C的方程；
（2）在圆C上，若到直线：的距离等于1的点恰有4个，求的取值范围．

如图，矩形ABCD的两条对角线相交于点M（3，5），AB边所在直线的方程为，点N（0，6）在AD边所在直线上．

（1）求AD边所在直线的方程；
（2）求对角线AC所在直线的方程．

已知圆：，点（1，  0），点在圆上运动， 的垂直平分线交于点．

（1） 求动点的轨迹的方程；
（2）设分别是曲线上的两个不同点，且点在第一象限，点在第三象限，若，为坐标原点，求直线的斜率；
（3）过点的动直线交曲线于两点，求证：以为直径的圆恒过定点

设命题：函数的定义域为；命题：当时，函数恒成立，如果命题“p∨q”为真命题，命题“p∧q”为假命题，求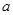的取值范围．

设O为坐标原点，点P的坐标（x－2，x－y）．
（1）在一个盒子中，放有标号为1，2，3的三张卡片，现从此盒中有放回地先后抽到两张卡片的标号分别记为x，y，求|OP|的最大值，并求事件“|OP|取到最大值”的概率；
（2）若利用计算机随机在[0，3]上先后取两个数分别记为x，y，求P点在第一象限的概率．

设命题p ：方程有两个不等的负实根； 命题q ：方程无实根． 若命题p或q为真命题，命题p且q为假命题，求实数m的取值范围．

某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示．

已知这100位顾客中一次购物量超过8件的顾客占55%．
（1）确定x，y的值，并求顾客一次购物的结算时间的平均值；
（2）求一位顾客一次购物的结算时间不超过2 min的概率．
（注：将频率视为概率）

已知：，：，若是的必要不充分条件，求实数m的取值范围．

（1）试用辗转相除法求840与1 764的最大公约数．
（2）利用秦九韶算法求多项式f（x）＝2x⁵＋4x⁴－2x³＋8x²＋7x＋4当x＝3的值，写出每一步的计算表达式．

设关于的一元二次方程
（Ⅰ）若是从0，1，2，3四个数中任取的一个数，是从0，1，2三个数中任取的一个数，
求上述方程有实数根的概率；
（Ⅱ）若是从区间任取的一个数，是从区间任取的一个数，求上述方程有实数根的概率．

设已知函数，．
（1）当时，求函数的最大值的表达式．
（2）是否存在实数，使得有且仅有3个不等实根，且它们成等差数列，若存在，求出所有的值，若不存在，说明理由．