某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示．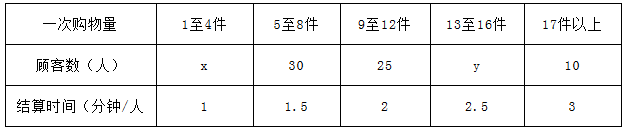
已知这100位顾客中一次购物量超过8件的顾客占55%．
（1）确定x，y的值，并求顾客一次购物的结算时间的平均值；
（2）求一位顾客一次购物的结算时间不超过2 min的概率．
（注：将频率视为概率）
相关试题
的前
项和为
,
. 
,求数列
的前
项和
.
，
.
；
与
、
均相切，切点分别为（
）、（
），且
，求证：
.
.
的单调区间；
与
有三个不同的交点，求实数
的取值范围.
.
的最小正周期；
在
处取得最大值，求
的值;
的单调递增区间.
为等差数列，且
.
项和
；
满足
求数列推荐套卷
某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示．
已知这100位顾客中一次购物量超过8件的顾客占55%．
（1）确定x，y的值，并求顾客一次购物的结算时间的平均值；
（2）求一位顾客一次购物的结算时间不超过2 min的概率．
（注：将频率视为概率）
粤公网安备 44130202000953号