设函数
(1)试判断当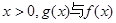 的大小关系;
的大小关系;
(2)求证: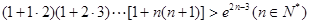 ;
;
(3)设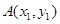 、
、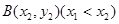 是函数
是函数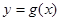 的图象上的两点,且
的图象上的两点,且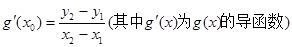 ,证明:
,证明: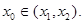
已知 、
、 分别是直线
分别是直线 和
和 上的两个动点,线段
上的两个动点,线段 的长为
的长为 ,
, 是
是 的中点.
的中点.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过点 任意作直线
任意作直线 (与
(与 轴不垂直),设
轴不垂直),设 与(1)中轨迹
与(1)中轨迹 交于
交于 两点,与
两点,与 轴交于
轴交于 点.若
点.若 ,
, ,证明:
,证明: 为定值.
为定值.
如图,已知空间四边形 中,
中, ,
, 是
是 的中点.
的中点.
求证:(1) 平面CDE;
平面CDE;
(2)平面 平面
平面
(3)若G为 的重心,试在线段AE上确定一点F, 使得GF//平面CDE.
的重心,试在线段AE上确定一点F, 使得GF//平面CDE.
已知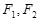 分别为椭圆
分别为椭圆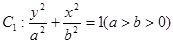 的上下焦点,其中
的上下焦点,其中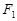 也是抛物线
也是抛物线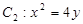 的焦点,点
的焦点,点 是
是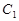 与
与 在第二象限的交点,且
在第二象限的交点,且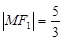 .
.
(1) 求椭圆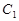 的方程;
的方程;
(2) 已知点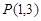 和圆
和圆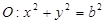 ,过点
,过点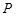 的动直线
的动直线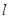 与圆
与圆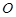 相交于不同的两
相交于不同的两
点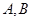 ,在线段
,在线段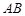 上取一点
上取一点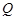 ,满足
,满足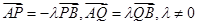 且
且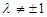 .
.
求证:点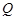 总在某定直线上.
总在某定直线上.
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
| 组别 |
理科 |
文科 |
||
| 性别 |
男生 |
女生 |
男生 |
女生 |
| 人数 |
4 |
4 |
3 |
1 |
学校准备从中选出4人到社区举行的大型公益活动进行采访,每选出一名男生,给其所在小组记1分,每选出一名女生则给其所在小组记2分,若要求被选出的4人中理科组、文科组的学生都有.(Ⅰ)求理科组恰好记4分的概率?
(Ⅱ)设文科男生被选出的人数为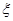 ,求随机变量
,求随机变量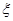 的分布列和数学期望
的分布列和数学期望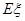 .
.
海岛B上有一座高为10米的塔,塔顶的一个观测站A,上午11时测得一游船位于岛北偏东15°方向上,且俯角为30°的C处,一分钟后测得该游船位于岛北偏西75°方向上,且俯角45°的D处.(假设游船匀速行驶)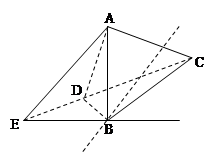
(1)求该船行使的速度(单位:米/分钟)
(2)又经过一段时间后,游船到达海岛B的正西方向E处,问此时游船距离海岛B多远.
已知不等式2|x-3|+|x-4|<2a.
(Ⅰ)若a=1,求不等式的解集;
(Ⅱ)若已知不等式的解集不是空集,求实数a的取值范围.
已知椭圆M: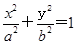 (a>b>0)的离心率为
(a>b>0)的离心率为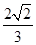 ,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.
(Ⅰ)求椭圆M的方程;
(Ⅱ)设直线l:x=ky+m与椭圆M交手A,B两点,若以AB为直径的圆经过椭圆的右顶点C,求m的值.
如图,在△ABC中,∠C=90°,BC=8,AB=10,O为BC上一点,以O为圆心,OB为半径作半圆与BC边、AB边分别交于点D、E,连接DE。
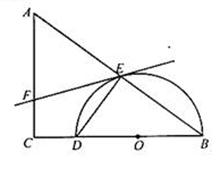
(1)若BD=6,求线段DE的长;
(2)过点E作半圆O的切线,交AC于点F,
证明:AF=EF。
如图,在四棱锥P—ABCD中,PA⊥底面ABCD,ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2。

(2)若∠PDC=120°,求四棱锥P—ABCD的体积。