(本小题满分10分)设 若A、B、C三点共线,
若A、B、C三点共线,
且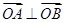 ,求
,求 的值.
的值.
已知不等式2|x-3|+|x-4|<2a.
(Ⅰ)若a=1,求不等式的解集;
(Ⅱ)若已知不等式的解集不是空集,求实数a的取值范围.
如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.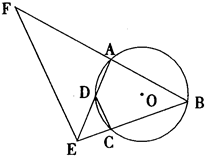
(Ⅰ)若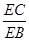 =
=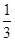 ,
,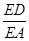 =
=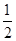 ,求
,求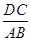 的值;
的值;
(Ⅱ)若EF2=FA·FB,证明:EF∥CD.
已知函数f (x)=lnx.
(Ⅰ)函数g(x)=3x-2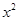 ,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
(Ⅱ)函数h(x)= ,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
G(x)<-2,求实数a的取值范围.
河南省某示范性高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座(规定:各科达到预先设定的人数时称为满座,否则称为不满座).统计数据表明,各学科讲座各天的满座概率如下表: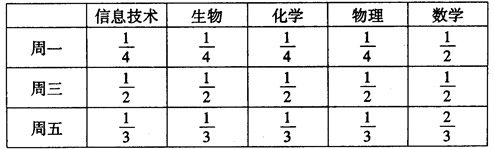
(Ⅰ)求数学辅导讲座在周一、周三、周五都不满座的概率;
(Ⅱ)设周三各辅导讲座满座的科目数为ξ,求随机变量ξ的分布列和数学期望.
已知函数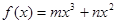 (
( 、
、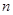 ∈R,
∈R, ≠0),函数
≠0),函数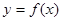 的图象在点(2,
的图象在点(2,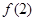 )处的切线与
)处的切线与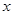 轴平行.
轴平行.
(1)用关于 的代数式表示
的代数式表示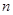 ;
;
(2)求函数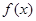 的单调增区间;
的单调增区间;
(3)当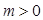 ,若函数
,若函数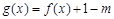 有三个零点,求m的取值范围.
有三个零点,求m的取值范围.
已知椭圆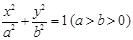 的一个焦点为F(2,0),离心率
的一个焦点为F(2,0),离心率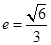 .
.
(1)求椭圆的方程;
(2)设直线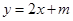 与椭圆交于不同的A,B两点,与y轴交于E点,且
与椭圆交于不同的A,B两点,与y轴交于E点,且 ,求实数m的值.
,求实数m的值.
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其重量(单位:克)是否合格,分别记录了6个抽查数据,获得重量数据的茎叶图如图4.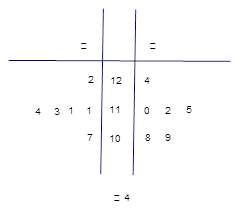
(1)根据样品数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对较稳定;
(2)若从乙车间6件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过2克的概率.
在极坐标系中,以点 为圆心,半径为3的圆
为圆心,半径为3的圆 与直线
与直线 交于
交于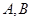 两点.(1)求圆
两点.(1)求圆 及直线
及直线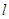 的普通方程.
的普通方程.
(2)求弦长 .
.
⑴已知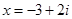 是关于
是关于 的方程
的方程 的一个根,求实数p和q的值.
的一个根,求实数p和q的值.
⑵已知 ,求
,求 .
.
已知函数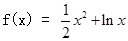
(1)求函数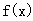 在区间
在区间 上的最大值和最小值,(
上的最大值和最小值,(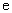 是自然对数的底数),
是自然对数的底数),
(2)求证:在区间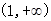 上,函数
上,函数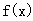 的图像在函数
的图像在函数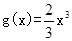 的图像的下方。
的图像的下方。