已知椭圆E的中心在坐标原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4; ,
, 是过点
是过点 且相互垂直的两条直线,
且相互垂直的两条直线, 交椭圆E于
交椭圆E于 ,
, 两点,
两点, 交椭圆E于
交椭圆E于 ,
, 两点,
两点, ,
, 的中点分别为
的中点分别为 ,
, .
.
(1)求椭圆E的标准方程;
(2)求直线 的斜率
的斜率 的取值范围;
的取值范围;
(3)求证直线 与直线
与直线 的斜率乘积为定值.
的斜率乘积为定值.
为综合治理交通拥堵状况,缓解机动车过快增长势头,一些大城市出台了“机动车摇号上牌”的新规.某大城市2012年初机动车的保有量为600万辆,预计此后每年将报废本年度机动车保有量的5%,且报废后机动车的牌照不再使用,同时每年投放10万辆的机动车牌号,只有摇号获得指标的机动车才能上牌.经调研,获得摇号指标的市民通常都会在当年购买机动车上牌.
(1)问:到2016年初,该城市的机动车保有量为多少万辆;
(2)根据该城市交通建设规划要求,预计机动车的保有量少于500万辆时,该城市交通拥堵状况才真正得到缓解.问:至少需要多少年可以实现这一目标.
(参考数据: ,
, ,
, ,
, )
)
如图所示,在四面体 中,
中, ,
, ,
, 两两互相垂直,且
两两互相垂直,且 .
.
(1)求证:平面 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
(3)若直线 与平面
与平面 所成的角为
所成的角为 ,求线段
,求线段 的长度.
的长度.
从某校高三年级800名学生中随机抽取50名测量身高.据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果分成八组得到的频率分布直方图如下:
(1)试估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为多少;
(2)在样本中,若学校决定身高在185cm以上的学生中随机抽取2名学生接受某军校考官进行面试,求:身高在190cm以上的学生中至少有一名学生接受面试的概率.
已知数列 的首项
的首项 ,前n项之和
,前n项之和 满足关系式:
满足关系式: .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 的公比为
的公比为 ,数列
,数列 满足
满足 ,且
,且 .
.
(i)求数列 的通项
的通项 ;
;
(ii)设 ,求
,求 .
.
△ABC中,AB=AC,M、N分别为AB、AC的中点,且 BN
BN CM,求△ABC的顶角
CM,求△ABC的顶角 的余弦值.
的余弦值.
已知 ,当k为何值时.
,当k为何值时.
(1) 与
与 垂直;
垂直;
(2) 与
与 平行,平行时它们是同向还是反向.
平行,平行时它们是同向还是反向.
如图,在棱长是1的正方体ABCD-A1B1C1D1中,点E,F,G分别是DD1,BD,BB1的中点. 
(1)求证:EF⊥CF;
(2)求EF与CG所成的角的余弦值;
(3)求三棱锥G-CEF的体积.
设二次函数 满足:(1)
满足:(1) 的解集是(0,1);(2)对任意
的解集是(0,1);(2)对任意 都有
都有 成立。数列
成立。数列
(I)求 的值;
的值;
(II)求 的解析式;
的解析式;
(III)求证: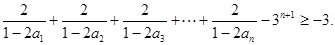
如图18图,已知AA1//BB1//CC1,且AA1=BB1=2CC1=2,AA1⊥面A1B1C1,△A1B1C1是边长为2的正三角形,M为BC的中点。
(1)求证:MA1⊥B1C1;
(2)求二面角C1—MB1—A1的平面角的正切值。