已知椭圆E的中心在坐标原点 ,焦点在
,焦点在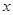 轴上,离心率为
轴上,离心率为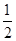 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;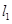 ,
,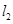 是过点
是过点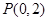 且相互垂直的两条直线,
且相互垂直的两条直线,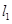 交椭圆E于
交椭圆E于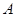 ,
,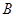 两点,
两点,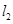 交椭圆E于
交椭圆E于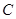 ,
,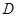 两点,
两点,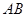 ,
,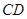 的中点分别为
的中点分别为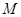 ,
,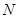 .
.
(1)求椭圆E的标准方程;
(2)求直线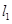 的斜率
的斜率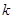 的取值范围;
的取值范围;
(3)求证直线 与直线
与直线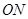 的斜率乘积为定值.
的斜率乘积为定值.
推荐套卷
已知椭圆E的中心在坐标原点 ,焦点在
,焦点在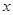 轴上,离心率为
轴上,离心率为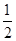 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;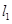 ,
,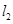 是过点
是过点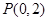 且相互垂直的两条直线,
且相互垂直的两条直线,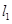 交椭圆E于
交椭圆E于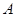 ,
,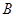 两点,
两点,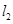 交椭圆E于
交椭圆E于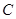 ,
,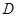 两点,
两点,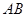 ,
,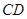 的中点分别为
的中点分别为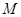 ,
,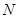 .
.
(1)求椭圆E的标准方程;
(2)求直线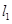 的斜率
的斜率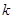 的取值范围;
的取值范围;
(3)求证直线 与直线
与直线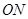 的斜率乘积为定值.
的斜率乘积为定值.